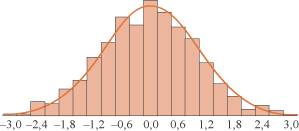
Variance et écart-type

Les deux séries de notes 8, 9, 11, 12 et 0, 9, 11, 20 ont la même médiane et la même moyenne, égales à 10 ; l'écart interquartile de ces deux séries est aussi identique.
Pour pouvoir différencier ces séries et prendre en compte les valeurs extrêmes de la seconde série, on est amené à introduire un nouveau paramètre de dispersion : l'écart-type.

1. Comment calculer la variance et l'écart-type ?

Pour quantifier la dispersion d'une série par rapport à sa moyenne, il semble naturel de calculer la moyenne des différences (ou des écarts) entre les valeurs observées et la moyenne, mais avec le risque d'obtenir des nombres négatifs qui, ajoutés à des nombres positifs, s'annulent. C'est pourquoi on a choisi de calculer la « moyenne des carrés des écarts à la moyenne ».

Telle est la définition de la variance V d'une série statistique.

Soit ni l'effectif correspondant à la valeur xi du caractère, alors V est définie par :

 .

L'écart-type  est défini, lui, comme la racine carrée de la variance :  .

C'est un paramètre particulièrement utilisé dans le cas de données dites gaussiennes.

2. Comment reconnaître si des données sont gaussiennes ?

Les données gaussiennes se caractérisent par une répartition en forme de cloche.

Elles ont l'allure suivante :

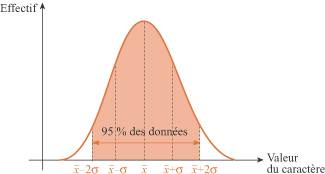
Dans le cas de données gaussiennes, la médiane et la moyenne sont confondues. La médiane est, de plus, le milieu de l'intervalle interquartile ; ainsi, le corps du diagramme qui représente les données est symétrique par rapport à la médiane.

3. Comment définir une plage de normalité, un niveau de confiance ?

Si une distribution statistique est gaussienne, de moyenne et d'écart-type , alors :

• environ 68 % des données sont dans l'intervalle  ;

• environ 95 % des données sont dans l'intervalle  ;

• environ 99,7 % des données sont dans l'intervalle .

Ces résultats montrent l'importance de l'écart-type. Ils nous permettent de définir les plages de normalité.

Ainsi, l'intervalle est la plage de normalité pour un niveau de confiance de 95 %. Notons qu'environ 1 donnée sur 20 se trouve à l'extérieur de cette plage.

On simplifie en admettant que l'intervalle est la plage de normalité pour un niveau de confiance de 99 % (au lieu de 99,7 %).

À retenir absolument

La variance V de la série statistique est égale à la moyenne des carrés des écarts à la moyenne.

Soit ni l'effectif correspondant à la valeur xi du caractère : .

L'écart-type  est la racine carrée de la variance : .

Des données sont gaussiennes lorsque le corps du diagramme qui les représente est symétrique par rapport à la médiane, et lorsque la médiane est égale à la moyenne.

Dans le cas de données gaussiennes, les intervalles et sont des plages de normalité pour des niveaux de confiance respectifs de 95 % et 99 %.