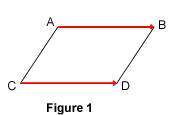
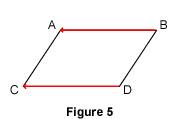
Utiliser les propriétés du parallélogramme liées à une égalité vectorielle

Les vecteurs sont définis à partir des translations. Les translations sont définies en classe de quatrième à partir des parallélogrammes. Les vecteurs sont donc liés aux parallélogrammes.

Mais de quelle façon ?

1. Parallélogramme et égalités vectorielles

1.1. Caractérisation d'un parallélogramme par une égalité vectorielle

En classe de quatrième, on définit ainsi la translation : si ABDC est un parallélogramme, alors la translation qui transforme A en B transforme aussi C en D.

Nous avons appris aussi que : si la translation qui transforme A en B transforme aussi C en D, alors .

Ces deux propriétés nous permettent d'énoncer la propriété suivante : si ABDC est un parallélogramme, alors .

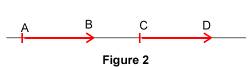
Réciproquement, si , alors ABDC est un parallélogramme.

Remarque : on notera que l'ordre des points C et D n'est pas le même dans le nom du parallélogramme et dans l'égalité vectorielle : ABDC et

Cas particulier : le parallélogramme ABDC peut être « aplati », ce qui correspond au cas où les points A, B, C et D sont alignés.

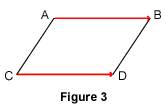
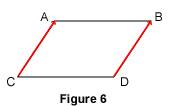
En résumé : signifie que ABDC est un parallélogramme (éventuellement aplati).

1.2. Égalités vectorielles obtenues à partir d'un parallélogramme

Considérons un parallélogramme ABDC : on en déduit l'égalité vectorielle .

Mais ce parallélogramme peut aussi être nommé ACDB ; on en déduit alors l'égalité vectorielle .

Si on nomme ce parallélogramme BACD, on déduit l'égalité vectorielle .

Si on nomme ce parallélogramme CABD, on déduit l'égalité vectorielle .

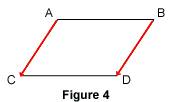
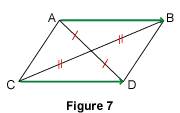
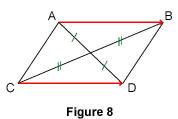
En résumé : un parallélogramme permet d'écrire quatre égalités vectorielles.

Observons les égalités et  : les vecteurs ont la même longueur, la même direction, mais pas le même sens. On dit que ce sont des vecteurs opposés.

Chaque égalité de deux vecteurs permet d'écrire l'égalité de leurs vecteurs opposés.

2. Égalité vectorielle et milieu

Nous avons vu dans le paragraphe précédent que si , alors ABDC est un parallélogramme.

Or on sait que, si un quadrilatère ABDC est un parallélogramme, alors ses diagonales [AD] et [BC] ont le même milieu. On en déduit donc la propriété suivante : si , alors les segments [AD] et [BC] ont le même milieu.

Réciproquement, si les segments [AD] et [BC] ont le même milieu, alors ABCD est un parallélogramme et .