Utiliser la règle et l'équerre

L'équerre, qui présente un angle droit, est l'instrument le plus approprié pour tracer des droites perpendiculaires. Avec l'équerre et la règle, on peut tracer des droites parallèles, en utilisant le fait que deux droites perpendiculaires à une même troisième sont parallèles entre elles.

1. Construire des perpendiculaires

1.1. Sans contrainte

On veut construire deux droites perpendiculaires quelconques. La figure suivante montre comment utiliser l'équerre pour réaliser cette construction.

1.2. Avec contrainte

Premier cas : l'une des deux droites est donnée.

Une droite d étant donnée, on veut construire une droite perpendiculaire à d. La méthode à utiliser est celle exposée dans le schéma précédent. Il est possible de construire une infinité de droites perpendiculaires à d ; il suffit de faire glisser l'équerre le long de d.

Second cas : l'une des deux droites est donnée et l'autre doit passer par un point donné.
Dans l'exemple de la figure suivante, on se donne une droite d et un point A extérieur à d. Il s'agit de construire la droite perpendiculaire à d passant par A.

On ne peut construire qu'une seule droite passant par un point donné et perpendiculaire à une droite donnée.

2. Construire des parallèles

2.1. Sans contrainte

On veut maintenant construire deux droites répondant à la seule contrainte d'être parallèles. La figure qui suit montre comment faire glisser l'équerre le long de la règle pour réaliser cette construction.

Les deux droites obtenues sont parallèles car on les a tracées perpendiculairement à la règle. On sait en effet que si deux droites d1 et d2 sont perpendiculaires à une même droite, alors d1 et d2 sont parallèles.

2.2. Avec contrainte

Premier cas : l'une des deux droites est donnée.

Une droite d étant donnée, on veut construire une droite parallèle à d. La méthode à utiliser est celle exposée dans le schéma précédent. Il est possible de construire une infinité de droites parallèles à d ; il suffit de changer la place de l'équerre contre la règle.

Second cas : l'une des deux droites est donnée et l'autre doit passer par un point donné.
Étant donnés une droite d et un point extérieur A à d, on doit mener la parallèle à d passant par A.

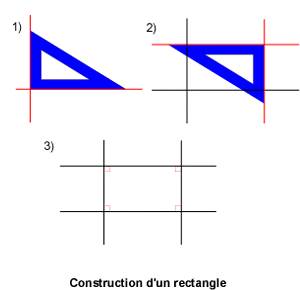
On ne peut construire qu'une seule droite passant par un point donné et parallèle à une droite donnée. Euclide, mathématicien grec du IIIe siècle av. J.-C., l'avait déjà affirmé (sous la forme de ce qu'on appelle un postulat) dans son ouvrage les Éléments.

3. Construire une figure avec la règle et l'équerre

On veut construire un rectangle avec une règle et une équerre. Voici comment on procède.