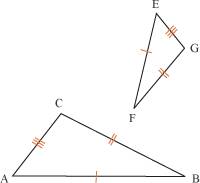
Triangles isométriques et triangles semblables

Par une suite de transformations qui conservent les distances, on transforme un triangle en un triangle qui lui est superposable ; on dit alors que ces triangles sont isométriques.

La notion de triangles isométriques se distingue de celle, plus large, de triangles semblables : deux triangles sont semblables s’ils ont des angles de mêmes mesures deux à deux.

1. Comment démontrer que deux triangles sont isométriques ?

Deux triangles sont isométriques s’ils sont superposables par glissement (translation ou rotation ) ou par retournement (symétrie axiale ou centrale).

Réciproquement, si les triangles ABC et EFG sont isométriques, il est alors possible de trouver une de ces transformations ou une suite de ces transformations, telle que l’image du triangle ABC soit le triangle EFG.

Pour démontrer que deux triangles sont isométriques, on utilise un des trois cas d’isométrie énoncés ci-dessous.

Ayant démontré que deux triangles sont isométriques, on peut facilement justifier des égalités de longueurs et/ou des égalités de mesures d’angles.

Exemple

ABC est un triangle scalène, ABDE et BCFG sont des carrés. On veut montrer que les côtés [CD] et [AG] ont la même longueur.

On sait que :

[AB] et [BD] sont deux côtés du carré ABDE, donc AB = BD ;

[BC] et [BG] sont deux côtés du carré ACFG, donc BC = BG ;

.

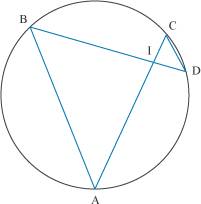
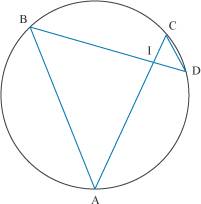
Les triangles ABG et BCD ont un angle de même mesure compris entre deux côtés de mêmes longueurs respectives donc, d’après le deuxième cas d’isométrie des triangles, ils sont isométriques.

On en déduit que les côtés [CD] et [AG] sont de la même longueur.

Remarquons que la transformation qui fait passer du triangle BDC au triangle BAG est la rotation de centre B, d’angle 90° dans le sens direct.

2. Comment démontrer que deux triangles sont semblables ?

On appelle triangles semblables (ou de même forme) des triangles dont les angles ont mêmes mesures deux à deux.

Pour démontrer que deux triangles sont semblables, il suffit de prouver que deux de leurs angles ont respectivement les mêmes mesures ; la somme des angles d’un triangle étant égale à 180°, la troisième égalité n’a pas besoin d’être démontrée.

Exemple

ABCD sont quatre points d’un cercle, [AC] coupe [BD] en I. On veut démontrer que les triangles AIB et CID sont semblables.

Les angles inscrits et interceptent le même arc BC, ils ont donc la même mesure ; il en est de même pour les angles inscrits et .

Les deux triangles AIB et CID ont deux angles respectivement de même mesure, donc ils sont semblables.

Remarque

Pour montrer que deux triangles sont semblables, on utilise aussi la réciproque du théorème fondamental des triangles semblables (voir ci-dessous) : si deux triangles ont des côtés correspondants de longueurs proportionnelles, alors ils sont semblables.

3. Que peut-on démontrer avec des triangles semblables ?

Deux triangles étant semblables, les longueurs de leurs côtés correspondants sont proportionnelles. Ce théorème fondamental permet de démontrer des égalités de rapports.

Exemples

ABC et EFG sont deux triangles semblables. Si on note k le rapport des longueurs des côtés de ces triangles, on a : . Si k > 1, k est un coefficient d’agrandissement ; si k < 1, k est un coefficient de réduction. Le rapport des aires des triangles EFG et ABC est alors .

ABCD sont quatre points d’un cercle, [AC] coupe [BD] en I et ID = 12 et IB = 36. On veut comparer les aires des triangles ABI et CDI.

Ces deux triangles sont semblables (voir l’exemple de la partie 2), leurs côtés sont donc proportionnels, c’est-à-dire : .

Le rapport de l’aire du triangle ABI et de l’aire du triangle CDI est égal à 3.

Donc aire(ABI) = 9 × aire(CDI).

À retenir absolument

Si deux triangles ont un côté de même longueur, adjacent à deux angles respectivement de mêmes mesures, alors ils sont isométriques.

Si deux triangles ont un angle de même mesure, situé entre deux côtés de mêmes longueurs respectives, alors ils sont isométriques.

Si deux triangles ont leurs trois côtés respectivement de mêmes longueurs, alors ils sont isométriques

Deux triangles sont semblables si et seulement si les longueurs de leurs côtés correspondants sont proportionnelles.

Si on note k le rapport des longueurs des côtés correspondants de deux triangles semblables, alors le rapport des aires des triangles est .