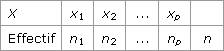
Simulations

Lorsque l'on jette un dé, la probabilité d'obtenir un « 5 » est de 1 chance sur 6. Ceci est parfaitement normal pour un dé non truqué.

Mais lorsqu'un inconnu sort deux dés de sa poche en proposant négligemment de jouer vos économies à la passe anglaise, comment peut-on être sûr que ces dés ne sont pas truqués ?

Si l'on lance 4 fois de suite l'un de ces dés et que l'on obtient 4 fois de suite le 5, doit-on penser que le dé est truqué ou est-ce simplement le hasard ? Doit-on encore relancer le dé avant de conclure ? Combien de lancers doit-on effectuer pour être sûr que le dé est ou n'est pas truqué, et, finalement, peut-on en être totalement sûr ?

1. Comment calculer une fréquence ?

Soit une série statistique :

ni est l'effectif de la valeur xi, c'est-à-dire le nombre de fois où la valeur xi est obtenue.
est la taille de la population.

fi est la fréquence de la valeur

La fréquence fi est un nombre compris entre 0 et 1 que l'on écrit parfois sous forme de pourcentage (par exemple, on écrit 74 % au lieu de 0,74).

On retrouve aussi cette notion de fréquence en probabilités. Soit A, un événement lié à une expérience aléatoire. On répète n fois cette expérience dans les mêmes conditions. Au cours de ces n répétitions indépendantes, on compte le nombre de fois où l'événement A est réalisé.

La fréquence de l'événement A est :

La fréquence de l'événement A tend vers la probabilité de l'événement A quand le nombre de répétitions tend vers .

Exemple :

On jette un dé 37 fois. Au cours de ces lancers, le 5 apparaît 12 fois. On en déduit alors que la

fréquence de l'événement « obtenir le 5 » est de

Si l'on jette maintenant le dé 3 700 fois, alors la fréquence de l'événement « obtenir le 5 » sera

proche de

2. Comment mesurer l'écart entre un échantillon et la répartition équiprobable ?

Considérons une épreuve aléatoire ayant k issues équiprobables : w1, w2, …, wk.

On répète n fois cette épreuve dans des conditions identiques ;  c'est ce que l'on appelle prélever un échantillon de taille n.

On note f1, f2, …, fk les fréquences d'apparition des issues w1, w2, …, wk lors de ces n

 répétitions. Ces fréquences sont assez proches de , sans être exactement égales à

Pour mesurer l'écart entre cet échantillon de taille n et l'échantillon théorique (pour lequel

toutes les fréquences sont égales à ), on calcule le nombre d2 défini par :

Pour tout n assez grand , on a alors pour au moins 95 % des échantillons de

taille n (ou pour moins de 5 % des échantillons de taille n).

3. Comment savoir si les issues d'une expérience sont équiprobables ?

Considérons une épreuve aléatoire ayant k issues : w1, w2, …, wk. Ces issues sont-elles équiprobables ?

On prélève un échantillon de taille n  (n   100) (autrement dit on répète n fois l'expérience dans des conditions identiques).

On calcule f1, f2, …, fk, les fréquences d'apparition des issues w1, w2, …, wk lors de ces n répétitions.

On calcule :

Si , l'échantillon est compatible avec l'hypothèse d'équiprobabilité. L'hypothèse d'équiprobabilité est plausible.

Si , l'échantillon est incompatible avec l'hypothèse d'équiprobabilité. L'hypothèse d'équiprobabilité est peu vraisemblable.

4. Comment, sur un exemple, construire et utiliser un test ?

Considérons une roue de loterie séparée en 4 secteurs égaux : un rouge, un bleu, un jaune et un vert.

Faisons tourner 150 fois cette roue et notons à chaque fois la couleur obtenue. On dit que l'on prélève un échantillon de taille 150. On peut s'attendre à ce que la fréquence d'apparition de chaque couleur soit assez proche de 0,25, sans être exactement égale à cette valeur.

On obtient les résultats suivants :

Fréquence du rouge :

Fréquence du bleu :

Fréquence du jaune :
Fréquence du vert :

Pour mesurer l'écart entre ces échantillons et l'échantillon théorique – pour lequel toutes les fréquences sont égales à 25 % –, on calcule le nombre d défini par :

Pour notre échantillon, on obtient :

d2 = (0,26 – 0,25)2 + (0,24 – 0,25)2 + (0,267 – 0,25)2 + (0,233 – 0,25)2 ;

On recommence avec un nouvel échantillon de taille 150 ;  on fait tourner la roue 150 fois et on mesure fr, fb, fj, fv ; on calcule d2. Quand on procède ainsi sur un grand nombre d'échantillons,

on constate que, dans plus de 95 % des cas,

On a maintenant le dispositif suivant : un cache, placé devant une roue que l'on fait tourner, nous montre simplement la couleur qui sort.

Le résultat est rouge, bleu, jaune ou vert. Mais comment les couleurs sont-elles réparties sur la roue cachée ? Les secteurs sont-ils égaux, comme précédemment, ou sont-ils inégalement partagés ?

Pour répondre à cette question, on prélève un échantillon de grande taille, de taille 100, par exemple.

Premier cas : on lance 100 fois la roue et on obtient les résultats ci-dessous.

Alors :

d2 = (0,28 – 0,25)2 + (0,26 – 0,25)2 + (0,21 – 0,25)2 + (0,25 – 0,25)2 ;

On constate que le résultat est identique à celui obtenu avec une roue à secteurs égaux. Dans ce cas, l'hypothèse d'équiprobabilité est plausible (il est plausible que la roue soit à secteurs égaux).

Second cas : on lance 100 fois la roue et on obtient les résultats ci-dessous.

Alors :

d2 = (0,37 – 0,25)2 + (0,18 – 0,25)2 + (0,22 – 0,25)2 + (0,23 – 0,25)2 ;

Ceci n'arrive que dans 5 % des cas quand la roue est à secteurs égaux. Dans ce cas, l'hypothèse d'équiprobabilité est peu vraisemblable : il est peu vraisemblable que la roue soit à secteurs égaux.

À retenir

Soit A, un événement lié à une expérience aléatoire. On réalise n répétitions indépendantes de cette expérience dans les mêmes conditions.

La fréquence de l'événement A est :

La fréquence de l'événement A tend vers la probabilité de l'événement A quand le nombre de répétitions tend vers l'infini.

Soit une épreuve aléatoire ayant k résultats équiprobables. On répète n fois cette épreuve dans des conditions identiques ;  c'est ce que l'on appelle prélever un échantillon de taille n.

La fréquence d'apparition d'un résultat pour l'ensemble de ces n répétitions est assez proche de