Séries chronologiques et tableaux à double entrée

Sont regroupés ici deux thèmes particuliers du programme de statistiques :

• en premier lieu, les séries chronologiques et la technique de lissage qui permet de dégager la tendance d’évolution d’une telle série statistique ;

• en second lieu, l’étude simultanée de deux variables statistiques sur une même population.

1. Comment reconnaître une série chronologique ?

Une série chronologique est une série de valeurs d’une même variable statistique X observée à intervalles réguliers dans le temps. Ces intervalles peuvent être en heures, en jours, en mois, en années, etc.

On a la présentation suivante :

L’étude d’une série chronologique permet de dégager une tendance générale d’évolution ou une périodicité malgré des variations irrégulières.

2. Comment lisser une série chronologique par les moyennes mobiles ?

Une technique pour dégager les grandes tendances d’une série chronologique consiste à remplacer chaque terme de la série par la moyenne de ce terme et de termes voisins. Lisser une série chronologique par les moyennes mobiles d’ordre 3 consiste à remplacer la série du tableau initial par le tableau suivant :

où : , avec .

Plus généralement, lisser une série chronologique par les moyennes mobiles d’ordre k consiste à remplacer la série initiale par la série des moyennes mobiles d’ordre k où chaque terme est remplacé par la moyenne arithmétique calculée sur les k termes voisins. En pratique :

• si , on remplace chaque terme par la moyenne de ce terme, des p termes qui précèdent et des p termes qui suivent ;

• si , on remplace chaque terme par la moyenne de ce terme, des p termes qui précèdent et des p termes qui suivent, mais en affectant aux termes extrêmes le coefficient .

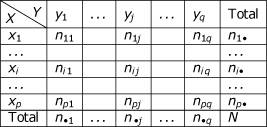
3. Comment établir le tableau de deux séries sur une même population ?

On étudie X et Y, deux variables statistiques qualitatives sur une même population de taille N.

Les valeurs, ou modalités, prises par X sont : .

Les valeurs, ou modalités, prises par Y sont : .

On présente dans un tableau à double entrée comment se répartissent les individus de la population :

N est l’effectif total de la population.

L’effectif correspondant à la i-ième ligne et la j-ième colonne est nij ; c’est le nombre d’individus prenant à la fois la modalité xi et la modalité yj.

La ligne et la colonne nommées « Total » sont appelées les distributions marginales. Elles reconstituent les séries statistiques X et Y sur notre population.

L’effectif de la modalité xi est , c’est le nombre d’individus prenant la modalité xi.

On a : .

L’effectif de la modalité yj est , c’est le nombre d’individus prenant la modalité yj.

On a : .

4. Comment calculer les fréquences marginales et conditionnelles ?

X et Y sont deux variables statistiques qualitatives sur une même population. On a :

La fréquence marginale de la modalité xi est égale à : .

La fréquence marginale de la modalité yj est égale à : .

La fréquence conditionnelle de la modalité xi dans la modalité yj (ou fréquence de xi sachant

yj) est égale à .

La fréquence conditionnelle de la modalité yj dans la modalité xi (ou fréquence de yj sachant xi)

est égale à .

À retenir absolument

Lisser une série chronologique par les moyennes mobiles d’ordre k consiste à remplacer la série initiale par la série des moyennes mobiles d’ordre k où chaque terme est remplacé par la moyenne arithmétique avec ses k termes voisins.

La fréquence marginale de la modalité xi est égale à  , où N est la taille de la population et est l’effectif de la modalité xi.

La fréquence conditionnelle de la modalité xi dans la modalité yj est égale à , où est l’effectif de la modalité yj et est le nombre d’individus prenant à la fois la modalité xi et la modalité yj.