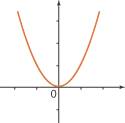
Sens de variation d'une fonction (B)

Du premier coup d’œil, on sait si une fonction affine est croissante ou décroissante, il suffit de voir si son coefficient directeur est positif ou négatif. Par ailleurs, si l’on a en mémoire les représentations graphiques des fonctions de référence (fonctions carré, inverse, racine et cube), on peut facilement se rappeler leur sens de variation.

D’autres fonctions plus complexes existent. Celles modélisant un coût, une dépense ou un bénéfice par exemple. Pour étudier les variations de telles fonctions, on cherche à les écrire sous la forme d’une somme ou de la composée de fonctions de base. À l’aide de quelques règles, on peut aisément en déduire leur sens de variation et ainsi connaître, par exemple, la production engendrant le coût minimal ou procurant le bénéfice maximal.

1. Comment déterminer le sens de variation d’une fonction sur un intervalle ?

Pour qu’une fonction f soit croissante sur un intervalle I, il faut que, pour tous nombres a et b de cet intervalle tels que a < b, on ait .

Plus directement, pour qu’une fonction soit croissante il faut et il suffit qu’elle respecte l’ordre : f(a) et f(b) doivent être rangés dans le même ordre que a et b sur l’intervalle I.

Si l’on a f(a) < f(b), c’est-à-dire une inégalité stricte, f est strictement croissante.

Pour qu’une fonction f soit décroissante sur un intervalle I, il faut que, pour tous nombres a et b de cet intervalle, tels que a < b, on ait .

Plus directement, pour qu’une fonction soit décroissante il faut et il suffit qu’elle inverse l’ordre : f(a) et f(b) doivent être rangés dans l’ordre inverse de celui de a et b sur l’intervalle I.

Si l’on a f(a) > f(b), la fonction f est strictement décroissante.

Pour qu’une fonction f soit constante sur un intervalle I, il faut que, pour deux nombres a et b de cet intervalle tels que a < b, on ait .

Plus directement, une fonction est constante sur un intervalle I lorsque tous les réels de cet intervalle ont la même image.

Remarque

Il ne faut pas confondre le sens de variation d’une fonction et son signe. Une fonction peut être positive et décroissante, c’est le cas pour la fonction carré sur l’intervalle . Elle peut aussi être négative et croissante, c’est le cas pour la fonction affine sur l’intervalle .

2. Quel est le sens de variation de la somme de deux fonctions monotones ? Qu’en est-il pour les autres opérations ?

Soit f et g deux fonctions croissantes sur un intervalle I. Pour deux nombres a et b de l’intervalle I tels que a < b on a :

f(a) < f(b) et g(a) < g(b).

Donc en additionnant membre à membre, on obtient :

f(a) + g(a) < f(b) + g(b).

C’est-à-dire, par définition de la fonction somme :

(f + g)(a) < (f + g)(b).

La fonction f + g est donc croissante.

On montre de même que si les deux fonctions sont décroissantes alors la fonction somme est décroissante.

En revanche, on ne peut rien dire du sens de variation de la fonction f + g lorsque f et g n’ont pas le même sens de variation.

Si > 0, f et f ont même sens de variation.

Si < 0, f et f ont des sens de variation opposés.

Pour les autres opérations, fonction différence f - g, produit fg et quotient , on ne peut pas conclure. Il faut raisonner à partir des écritures de ces fonctions.

3. Quel est le sens de variation des fonctions de référence ?

Pour connaître le sens de variation des fonctions de référence, il suffit de savoir tracer leur représentation graphique.

Fonction carré

est décroissante pour

est croissante pour

Fonction racine

est croissante pour

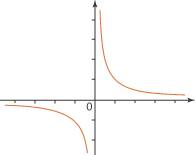
Fonction inverse

est décroissante pour x < 0

est décroissante pour x > 0

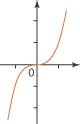
Fonction cube

est croissante sur

4. Quel est le sens de variation d’une fonction composée ?

Soit deux fonctions :

• f définie sur un intervalle I à valeurs dans un intervalle J ;

• g définie sur J.

La fonction , composée de f, suivie de g, est une fonction définie sur I. Son sens de variation dépend des sens de variation de f et g. Il est donné par le tableau suivant :

Si les deux fonctions monotones données ont le même sens de variation, alors la fonction composée est croissante.

Si les deux fonctions ont des sens de variation opposés, la fonction composée est décroissante.

À retenir absolument

Si deux fonctions monotones ont le même sens de variation sur un intervalle, leur fonction somme a le même sens de variation.

La composée de deux fonctions monotones de même sens de variation est croissante.
Si les sens de variation sont opposés, elle est décroissante.