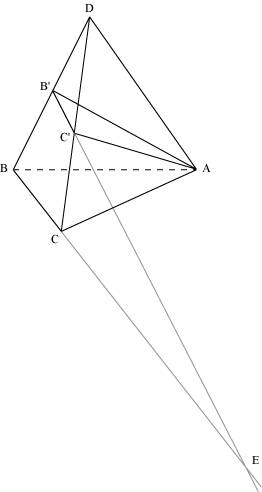
Sections planes

Une des difficultés de la géométrie dans l'espace est d'arriver à représenter sur une feuille de papier, de dimension deux, un objet de l'espace en trois dimensions. C'est pour répondre à cette difficulté que les géomètres ont inventé, en particulier, la perspective cavalière.

1. Quelles sont les règles à connaître pour représenter un solide de l'espace en perspective cavalière ?

Un dessin en perspective cavalière montre ce que l'on voit dans un plan vertical perpendiculaire aux rayons visuels.

Par conséquent, les figures situées dans un plan perpendiculaire aux rayons visuels (plan frontal) sont représentées en vraie grandeur : on respecte les longueurs et les angles.

La perspective cavalière conserve le parallélisme des droites et le milieu des segments. De plus, si deux segments inclus dans des droites parallèles ont même longueur, alors ils sont représentés par deux segments qui ont aussi même longueur.

Pour tracer une droite perpendiculaire à une face frontale (par exemple dans un cube), on représente une droite faisant avec l'horizontale un angle appelé angle de perspective ou angle de fuite et que l'on choisit souvent de 45°, de 30° ou de 60°.

Toutes les longueurs des segments qui ne sont pas dans le plan frontal sont réduites. Sur les droites perpendiculaires au plan frontal, elles sont multipliées par un coefficient k, tel que , appelé coefficient de perspective.

Enfin, les droites non visibles de la figure sont représentées en lignes pointillées.

2. Comment représenter la section d'un solide par un plan, en perspective cavalière ?
Pour représenter la section d'un solide par un plan, on détermine les droites d'intersection du plan avec chacune des faces du solide, ce qui revient à se ramener au problème de la détermination de l'intersection de deux plans.

Cette représentation repose sur deux principes assez simples énoncés ci-dessous.

Utilisation des propriétés d'incidence. Dès qu'on connaît deux points communs à un plan P et au plan contenant une face d'un solide, on connaît l'intersection du plan P et de la face du solide.

En effet, si deux points A et B appartiennent à un plan P, alors la droite (AB) est incluse dans le plan P.

Si une droite D est incluse dans un plan P et si une droite D' est incluse dans un plan P', alors le point d'intersection de D et de D' appartient à l'intersection de P et de P'.

Si deux plans sont parallèles, tout plan qui coupe l'un coupe l'autre et les droites d'intersection sont parallèles.

Si deux plans sécants sont parallèles à une même droite D, alors leur droite d'intersection est parallèle à la droite D.

Utilisation des tracés hors solide. On remarque qu'on ne s'intéresse pas seulement à l'intersection d'un plan P avec la face du solide mais à l'intersection du plan P avec le plan contenant la face du solide. Il peut donc arriver que les points nécessaires pour représenter la section du solide par le plan ne fassent pas partie du solide. Ceci signifie qu'il ne faut pas hésiter à prolonger les tracés.

3. Comment représenter en vraie grandeur la section d'un solide par un plan ?

On a vu que, sauf si elles sont dans un plan frontal, les figures planes ont leur représentation changée par la perspective cavalière (par exemple, le carré de base d'un cube est représenté par un parallélogramme non carré).

On peut, dans certains cas, avoir besoin de représenter la section du solide par un plan en « vraie grandeur », de manière à pouvoir ensuite se ramener à un problème de géométrie plane.

Pour cela, on peut :

• représenter le solide de façon à ce que la section cherchée se trouve dans le plan frontal et soit ainsi obtenue directement en vraie grandeur ;

• déterminer la nature de cette figure (triangle, quadrilatère, etc.), puis calculer les distances et les angles. On est alors ramené à un problème de construction de géométrie plane ;

• repérer dans la figure en perspective des segments de même longueur ou des angles égaux dont l'un est dans un plan frontal, ce qui permet d'en connaître la vraie grandeur. On revient ensuite à la méthode précédente.

À retenir absolument

On représente les solides et les figures de l'espace en perspective cavalière ; seules les figures incluses dans un plan frontal sont alors représentées en vraie grandeur.

Déterminer la section d'un solide par un plan P, c'est déterminer l'intersection du plan P avec chacun des plans contenant les faces du solide.

Pour déterminer l'intersection du plan P avec une des faces du solide, il suffit de déterminer deux points de cette intersection.