Représenter la section d'une sphère par un plan

Pour préparer une orange givrée, on commence par couper une orange avec un couteau. La trace laissée par le couteau sur l'écorce est appelée en mathématiques une section (le mot section vient du latin secare qui signifie « couper »). L'objectif ici est de représenter la section d'une sphère (l'écorce) par un plan (le plan de coupe du couteau), c'est-à-dire l'intersection d'une sphère et d'un plan.

1. Les différents cas possibles

Il paraît évident que si le plan est très éloigné de la sphère, il ne la coupera pas. La section d'une sphère par un plan dépend en effet de la distance du plan au centre de la sphère. Il faut donc d'abord définir ce qu'on appelle la distance d'un plan à un point.

Définition : soit P un plan et O un point de l'espace. H est le point d'intersection de la droite D perpendiculaire à P passant par O. La distance OH est appelée distance du point O au plan P.

Remarque : H est le point de P qui est le plus proche de O.

Considérons maintenant une sphère de centre O et de rayon r et un plan P. H étant défini comme précédemment, on peut dire que OH est la distance du plan P au centre O de la sphère.

Pour l'étude de la section de la sphère par P, nous allons distinguer trois cas.

1.1. Cas où OH > r

Le plan P est alors suffisamment éloigné de la sphère pour ne pas la couper, comme on peut l'observer sur la figure 2. Dans ce cas, le plan et la sphère n'ont aucun point commun.

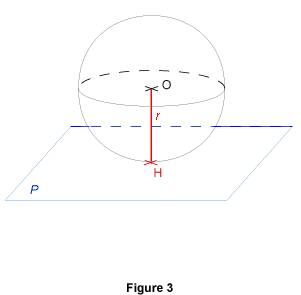
1.2. Cas où OH = r

Dans ce cas, le point H se trouve sur la sphère, et c'est le seul point commun à la sphère et au plan (voir la figure 3). On dit alors que la sphère et le plan sont tangents, comme on le dit d'une droite et d'un cercle qui n'ont qu'un point commun.

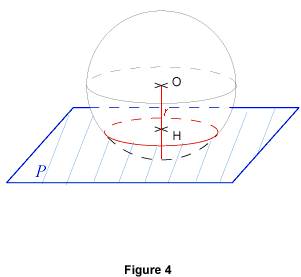
1.3. Cas où OH < r

Dans ce cas, le plan coupe vraiment la sphère. L'intersection du plan et de la sphère est un cercle de centre H.

Remarque : plus le plan P est proche de O, plus le rayon de la section est grand. Il est d'ailleurs possible de calculer le rayon de la section si on connaît la distance OH et le rayon de la sphère.

2. Sections remarquables de la sphère terrestre

Sur la figure 5, la Terre sous la forme d'une sphère, où les points N et S (qui sont diamétralement opposés) représentent les pôles Nord et Sud. La droite (NS) est appelée l'axe des pôles. Nous allons maintenant voir qu'en coupant la Terre suivant des plans particuliers, on obtient des sections connues des géographes :

Si on coupe la Terre par un plan perpendiculaire à l'axe des pôles et passant par le centre, la section obtenue est un grand cercle terrestre bien particulier : l'équateur.

Si on coupe la Terre par un plan perpendiculaire à l'axe des pôles, la section obtenue est un cercle parallèle.

Si on coupe la Terre par un plan passant par l'axe des pôles, la section obtenue est un grand cercle de diamètre [NS], formé de deux méridiens.

Figure 5