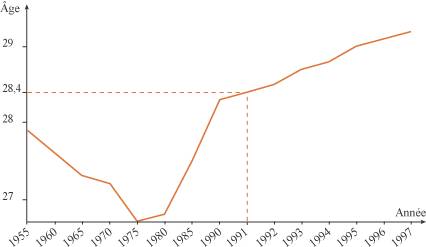
Représentations graphiques

Un graphique permet d'appréhender facilement une situation, de percevoir d'un seul coup d'œil un ensemble de données, de comparer deux situations en étudiant la position relative de deux courbes. Il existe plusieurs manières de représenter les mêmes données, chacune mettant en avant ou en retrait certaines caractéristiques. Comment lire et interpréter correctement un graphique ? Quels éléments influent sur une représentation graphique ?

1. Comment lire un graphique dans un repère du plan ?

Pour cela, il est nécessaire de revoir le vocabulaire mathématique relatif aux représentations graphiques. Prenons l'exemple du graphique ci-dessous qui représente l'âge moyen des femmes à la maternité de 1955 à 1997.

La courbe représente la fonction f qui, à toute année x, associe l'âge moyen f(x) à la première naissance. Cette fonction est définie sur l'intervalle [1955 ; 1997].

L'image de 1991 par la fonction f est 28,4. L'antécédent de 28,4 par f est 1991.

2. Comment lire et représenter les variations d'une courbe ?

Reprenons l'exemple ci-dessus. On dit que la fonction f est décroissante sur l'intervalle [1955 ; 1975] et croissante sur l'intervalle [1975 ; 1997].

Ces informations peuvent être résumées dans le tableau de variations suivant :

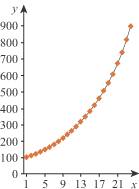
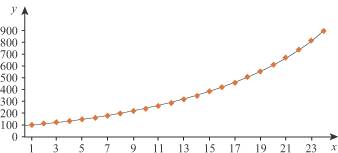
3. Qu'est-ce qu'un changement de fenêtre graphique ?

Lorsque l'on doit représenter graphiquement des données, il faut d'abord choisir une échelle pour l'axe des abscisses et l'axe des ordonnées. Il y a plusieurs possibilités qui correspondent à plusieurs fenêtres graphiques. Les deux courbes ci-dessous représentent les mêmes données dans deux fenêtres graphiques différentes.

4. Comment lire un graphique dans un repère de l'espace ?

On sait que, dans le plan, il suffit de deux nombres pour repérer un point M : l'abscisse x et l'ordonnée y.

Dans l'espace, il en faut un troisième : la cote z. Les repères de l'espace se présentent généralement sous la forme suivante :

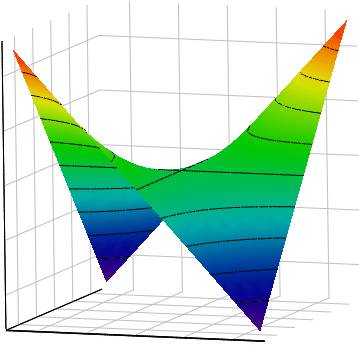
5. Qu'appelle-t-on courbes de niveau ?

Considérons la surface d'équation z = xy représentée dans le repère de l'espace ci-dessous.
Un point M de cette surface dont l'abscisse est x et l'ordonnée y a pour cote z = xy, on le note M(x ; y ; xy).

Les points de cette surface qui ont la même cote z forment des courbes appelées courbes de niveau. Elles sont dessinées en noir sur la représentation précédente.

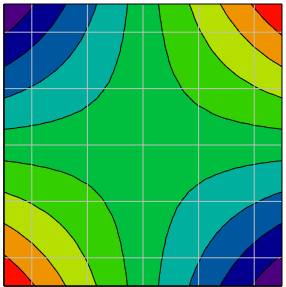
Les courbes de niveau sont très utilisées en cartographie, car elles permettent de représenter dans le plan la surface d'un relief. Il suffit pour cela de relier les points de cette surface qui ont la même cote.

Dans l'exemple ci-dessous, qui est une vue en plan de la surface précédente, les points des zones bleues à vertes ont une cote comprise entre -25 et 0. Les différentes zones colorées sont ici délimitées par les courbes de niveau : z = -25 ; z = -20 ; z = -15 ; jusqu'à z = 25.