Reconnaître la proportionnalité sur un graphique

Quand on parle de la médiatrice d'un segment, on pense aux mots milieu, perpendiculaire et équidistant. Quelles sont donc les caractéristiques de cette droite et comment la construit-on ?

1. Reconnaître la médiatrice d'un segment
1.1. Définition
La médiatrice d'un segment est la droite qui est perpendiculaire à ce segment et qui passe par son milieu.

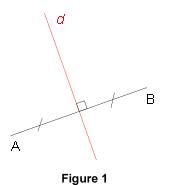
La médiatrice d'un segment est un axe de symétrie de ce segment.

1.2. Propriété
La médiatrice d'un segment est l'ensemble des points du plan qui sont équidistants des extrémités de ce segment. Si l'on considère un segment [AB], tout point de la médiatrice est à la même distance de A et de B.

Par exemple, sur la figure 2, le point M, qui appartient à la médiatrice de [AB], est situé à 4 cm de A et 4 cm de B, le point N à 2,5 cm de A et 2,5 cm de B.

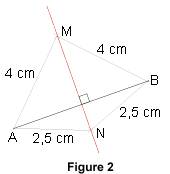
Réciproquement, si un point est à la même distance de A et de B, alors ce point appartient à la médiatrice de [AB].
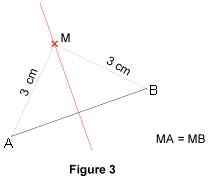
Par exemple, sur la figure 3, le point M, qui est à la même distance de A et de B (à 3 cm), appartient à la médiatrice de [AB].

2. Construire la médiatrice d'un segment
2.1. Avec le compas
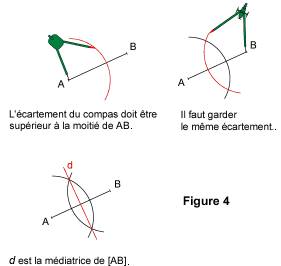
La série de figures ci-dessous montre les étapes de la construction. On peut adapter celles-ci en fonction des mesures données.
Les deux points utilisés pour tracer la médiatrice sont équidistants des extrémités du segment ; en effet, on a utilisé le même écartement de compas pour tracer les arcs de cercle.

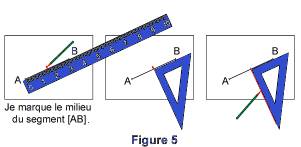
2.2. Avec la règle graduée et l'équerre
La série de figures ci-dessous montre les étapes de construction. On peut adapter celles-ci en fonction des mesures données.