 |
||||||
| Institut THOMASTA : Quelles seront les nouvelles technologies de demain ? | ||||||
|
||||||
|
||||||
Probabilités et dénombrement Depuis leur entrée dans l'univers des mathématiques (avec Blaise Pascal au xviie siècle), les probabilités ont pris une place croissante dans notre façon d'appréhender le monde. La mécanique quantique, par exemple, repose en partie sur le calcul des probabilités. Le programme de terminale se limite à l'étude des cas où le nombre de résultats possibles est fini et à quelques exemples de lois continues. 1. Comment définir et calculer une probabilité ? À partir d'une expérience aléatoire E, on définit l'univers Définir une probabilité sur E, c'est associer à chacun des résultats possibles On peut déterminer les nombres — soit statistiquement : a alors pour un événement A quelconque : — soit par hypothèse d'équiprobabilité : Dans ce dernier cas, on est amené à dénombrer, c'est-à-dire à compter le nombre d'éléments d'un ensemble. Pour cela, on utilise des techniques assez simples comme les arbres, les diagrammes, les tableaux à double entrée. 2. Comment compter le nombre de tirages successifs, avec remise ? Le modèle de référence dans ce cas est celui d'une urne contenant n jetons numérotés dont on extrait p jetons, en remettant après chaque tirage le jeton tiré dans l'urne. Combien de résultats différents peut-on obtenir lors de cette expérience ? On peut fabriquer un arbre ou simplement tenir le raisonnement suivant :
On en déduit que le nombre de résultats possibles est : 3. Comment compter le nombre de tirages successifs, sans remise ? Le modèle de référence dans ce cas est celui d'une urne contenant n jetons numérotés dont on extrait p jetons Là encore, on peut fabriquer un arbre ou recommencer notre raisonnement :
On en déduit que le nombre de résultats possibles est : où n! est le nombre Cas particulier : Si l'on fait n tirages sans remise dans l'urne et que l'on vide l'urne, alors le nombre de résultats possibles est n!. C'est aussi le nombre de façons de ranger n objets les uns par rapport aux autres. 4. Comment compter le nombre de tirages simultanés ? Si l'on extrait p jetons simultanément (c'est-à-dire sans ordre ni répétition) de l'urne contenant n jetons numérotés, le nombre de tirages possibles ou nombre de combinaisons est alors : 5. Comment développer (a + b)n ? Les propriétés des combinaisons sont les suivantes : La dernière propriété permet d'établir le triangle de Pascal qui, de proche en proche, donne les valeurs des nombres Connaissant ces nombres, on peut développer (a + b)n à l'aide du binôme de Newton : 6. Comment calculer une probabilité sans passer par le dénombrement ? Connaissant les probabilités de certains événements, on peut en trouver d'autres à l'aide des propriétés suivantes :
À retenir Définir une probabilité, c'est associer, à chacun des résultats xi de l'expérience aléatoire, un nombre pi positif tel que la somme des pi soit égale à 1. Dans une situation d'équiprobabilité, la probabilité d'un événement A quelconque est : Soit une urne contenant n jetons numérotés dont on extrait p jetons :
Soit une urne contenant n jetons numérotés dont on extrait p jetons simultanément, le nombre de résultats possibles est :
|
||||||
|
Prof.: Thomas TAMENOU - Thomasta.com -
Contactez-nous |
||||||
 |
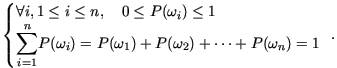
 (généralisation des « identités remarquables »).
(généralisation des « identités remarquables »).