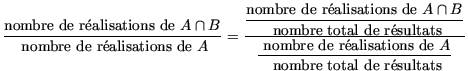Probabilités conditionnelles (Terminale)

Si je jette un dé non truqué, la probabilité d'obtenir un 6 est de Si je lance ce même dé, qu'une tierce personne me cache le résultat et me dise « j'ai vu que le résultat est pair », la probabilité de l'événement « avoir un 6 » devient J'ai tenu compte de l'information donnée. On dit que la probabilité d'obtenir 6, sachant que le nombre obtenu est pair, est ; il s'agit d'une probabilité conditionnelle.

1. Comment calculer une probabilité conditionnelle ?

Soit A et B, deux événements quelconques de probabilités non nulles.

Si je sais que l'événement A est ou va être réalisé, alors :

• les résultats possibles se réduisent à ceux qui réalisent A ;

• les résultats qui réalisent B se réduisent à ceux qui réalisent à la fois A et B.

La « probabilité de l'événement B, sachant que l'événement A est réalisé », notée PA(B)

ou P(B/A), est alors

Or :

Soit :

On calcule donc une probabilité conditionnelle à l'aide de la définition suivante :

On retrouve, sur les probabilités conditionnelles, les propriétés habituelles d'une probabilité, c'est-à-dire :

 ; 

2. Comment passer de PA(B) à PB(A) ?

Très souvent, dans la pratique comme dans les problèmes posés, on connaît PA(B) et on veut trouver soit , soit PB(A).

Pour obtenir ces probabilités, il suffit de repartir de la définition précédente.

Soit A et B, deux événements quelconques de probabilités non nulles.

On a : d'où

Mais on a aussi : d'où

Et comme , on obtient :

Ce qui nous donne au final :

3. Comment montrer que deux événements sont indépendants ?

Intuitivement, deux événements sont indépendants si la réalisation de l'un de ces événements n'influe pas sur la probabilité de l'autre.

On doit donc avoir : PA(B) = P(B).

C'est-à-dire

A et B sont donc indépendants si et seulement si

Si deux événements A et B sont indépendants, alors :

• et B sont indépendants ;

• et sont indépendants ;

• A et sont indépendants.

La notion d'indépendance pose souvent problème car on l'utilise dans les deux « sens » :

• dans certains cas, on dira : il est évident que A et B sont indépendants donc Ce cas de figure se présente lorsque A et B sont issus de deux expériences séparées ou de deux répétitions distinctes d'une même expérience, réalisées dans des conditions identiques ;

• dans d'autres cas, on dira : , donc A et B sont indépendants. C'est d'ailleurs la réponse que l'on attend quand on pose la question : A et B sont-ils indépendants ?

Remarque :

Attention à ne pas confondre :

• A et B incompatibles (c'est-à-dire :  ;

• A et B indépendants (c'est-à-dire : ).

4. Comment utiliser la formule des probabilités totales ?

La formule des probabilités totales repose sur l'existence d'une partition.

Les événements réalisent une partition de l'univers  si, pour tous nombres i et j compris entre 1 et n :

 ;

, pour  ;

Cas particulier important : si B est un événement avec et , alors B, forment une partition.

Ayant une partition B1, B2,…, Bn de l'univers , on considère un événement A quelconque. On peut écrire que les événements élémentaires qui réalisent A sont les événements élémentaires de B1 qui réalisent A « union » les événements élémentaires de B2 qui réalisent A « union » … « union » les événements élémentaires de Bn qui réalisent A.

C'est-à-dire :

D'où la première expression de la formule des probabilités totales :

Et comme , on obtient la seconde expression de la formule des probabilités totales :

À retenir

Soit A et B deux événements de probabilités non nulles. La probabilité de l'événement A, sachant que l'événement B est réalisé, est appelée probabilité conditionnelle. Elle est définie

par :

Les événements A et B sont indépendants lorsque la réalisation de l'un de ces événements n'influe pas sur la probabilité de l'autre. A et B sont donc indépendants si et seulement si :

À partir d'une partition, on peut utiliser la formule des probabilités totales.