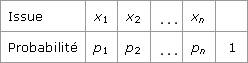
Probabilités (Terminale)

Que faut-il savoir pour aborder le chapitre des probabilités en terminale ? Il faut d'abord savoir définir une probabilité, il faut également être capable de calculer la probabilité d'un événement, soit à partir de la définition, soit à partir des propriétés des probabilités.

Enfin, il est nécessaire de maîtriser la technique d'élaboration d'un arbre, celle-ci étant adaptée pour calculer des probabilités conditionnelles et modéliser les répétitions d'une même expérience.

1. Comment définir une probabilité ?

On définit une probabilité en deux temps :

• à partir d'une expérience aléatoire, on définit l'univers associé , c'est-à-dire l'ensemble des issues possibles de l'expérience ;

• à chaque issue xi, on associe un nombre pi, avec , de telle sorte que p1 + p2 + ... + pn = 1 ; pi est appelé probabilité de l'issue xi.

Pour déterminer pi, il existe deux possibilités :

soit on associe à toutes les issues la même probabilité On dit alors que la probabilité est équirépartie ou que l'on est dans une situation d'équiprobabilité ;

soit on répète l'expérience dans des conditions identiques et on définit pi comme la fréquence de xi, quand le nombre de répétitions tend vers .

Remarque :

Il s'agit d'abord de bien comprendre l'expérience, de la visualiser, de la simuler pour écrire quelques issues possibles, puis enfin de déterminer toutes les issues de l'expérience. C'est dans la détermination de toutes ces issues que réside la difficulté. On utilise souvent pour les trouver soit des arbres, soit des tableaux.

2. Comment calculer la probabilité d'un événement ?

On a préalablement défini l'univers  , c'est-à-dire l'ensemble des issues possibles de l'expérience, ainsi que la probabilité de chacune de ces issues. On a donc :

Un événement A est une partie de . Quand xi appartient à A, on dit aussi que xi réalise A.
On distingue des événements particuliers :

• —  est appelé événement impossible ;

• —  est appelé événement certain ;

• — A = {xi}, événement constitué d'une seule issue, est appelé événement élémentaire.

La probabilité de l'événement A, notée P(A), est égale à la somme des probabilités des issues qui réalisent A.

Dans le cas où la probabilité est équirépartie, on a :

3. Comment utiliser les propriétés d'une probabilité ?

Soit A et B, deux événements d'une même expérience aléatoire.

est l'événement constitué des issues qui appartiennent à A ou à B.

est l'événement constitué des issues qui appartiennent à la fois à A et à B.

Quand , c'est-à-dire quand aucune issue n'appartient à la fois à A et à B, on dit que A et B sont incompatibles.

est l'événement contraire de A ; il est constitué des issues qui n'appartiennent pas à A.
Connaissant la probabilité de certains événements, on peut calculer la probabilité d'autres événements sans être obligé de passer par la définition :

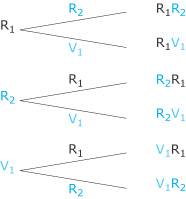
P(A) = somme des probabilités des issues qui constituent A.

On utilise alors les propriétés ci-dessous :





si A et B sont incompatibles :  ;

4. Comment élaborer un arbre ?

Quand une expérience aléatoire peut être décomposée en une suite d'expériences aléatoires plus simples, l'élaboration d'un arbre est l'outil le plus simple pour obtenir l'ensemble des issues possibles. Pour chacune des expériences aléatoires de base, on trace une branche par issue possible. La lecture de tous les chemins permet ensuite d'obtenir toutes les issues possibles.

Exemple :

Une urne contient 2 jetons rouges et 1 jeton vert. On fait, dans cette urne, deux tirages successifs sans remise. Quelles sont les issues possibles de cette expérience ?

On numérote les jetons R1, R2, V1. Chaque jeton à la même probabilité d'être choisi, on a donc une situation d'équiprobabilité (ce n'est pas le cas si l'on considère les couleurs, la probabilité d'obtenir un jeton rouge n'est pas la même que la probabilité d'obtenir un jeton vert).

On décompose l'expérience en premier jeton tiré, deuxième jeton tiré.

On obtient alors l'arbre suivant :

D'où : .

Remarque :

On peut procéder de même pour des tirages avec remise ou pour des tirages simultanés.

À retenir

Définir une probabilité, c'est associer à chacun des résultats de l'expérience aléatoire xi un nombre pi positif tel que la somme des pi soit égale à 1.

Un événement A est une partie des résultats d'une expérience aléatoire. La probabilité de l'événement A est la somme des probabilités des résultats qui réalisent A.

Dans une situation d'équiprobabilité, la probabilité de l'événement A est :