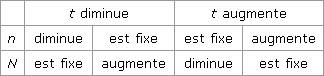
Pourcentages (1re)

La notion de pourcentage intervient dans de nombreux domaines. Il est aisé de calculer une quantité lorsque l’on connaît le pourcentage qu’elle représente par rapport à une quantité totale. Mais qu’en est-il si l’on cherche une quantité résultant de variations successives en pourcentage ? Comment déterminer le pourcentage global d’évolution ? Dans quels cas est-il possible de trouver facilement une approximation de ce pourcentage ?

1. Comment calculer ou appliquer un pourcentage ?

Pour calculer le pourcentage que représente une quantité n par rapport à une quantité totale N

, il suffit de calculer le quotient , puis de le multiplier par 100.

Par exemple, s’il y a 18 filles dans une classe de 31 élèves, le pourcentage de filles dans la

classe est , soit environ 58 %.

On sait que calculer t % d’une quantité revient à la multiplier par .

De la même manière, calculer t’ % de t % d’une quantité revient à la multiplier par .

Par exemple, calculer 50 % de 50 % d’une quantité revient à la multiplier par donc à calculer 25 % de cette quantité.

2. Comment calculer une quantité finale après une hausse ou une baisse de t % ?

On calcule t % de la quantité et l’on ajoute ou retranche ce résultat à la quantité initiale.

Ainsi, pour une hausse de t %, si P est la quantité initiale et P’ la quantité finale, on obtient :

. Soit .

On peut donc calculer directement le coefficient multiplicatif associé à une augmentation ou à une hausse de t %.

Pour une baisse de t %, le coefficient multiplicatif est .

Par exemple, si un article qui coûte 40 € est soldé à 30 %, son nouveau prix, en €, sera , soit 28 €.

3. Comment calculer une quantité après plusieurs variations en pourcentage ?

Si l’on fait varier une quantité de t %, puis de t’ %, on obtient la quantité finale en

multipliant la quantité initiale par : .

Par exemple, augmenter un prix de 20 % puis le baisser de 10 % revient à le multiplier par 1,2 × 0,9.

De manière analogue, appliquer n fois le même pourcentage revient à multiplier n fois par

, donc à multiplier par .

Par exemple, augmenter une production de 4 % par an pendant 10 ans revient à multiplier cette production par (1,04)10.

4. Qu’est-ce qu’une approximation linéaire ?

Lorsqu’un nombre a est suffisamment petit, (1 + a)n est voisin de 1 + na.

Ainsi, le coefficient multiplicatif associé à n augmentations de t % : est voisin de , si t est suffisamment petit. C’est ce dernier terme qui est appelé approximation linéaire.

Par exemple, augmenter un prix de 4 % par an pendant 10 ans revient à le multiplier approximativement par 1,4.

5. Comment déterminer un pourcentage d’évolution ?

Lorsque la valeur initiale est x0 et la valeur finale x1, le pourcentage t d’évolution est donné

par la relation : .

Par exemple, un prix qui est passé, en 5 ans, de 82 € à 50 € a subi une variation de

, soit une baisse de 64 %.

Lorsque l’on veut déterminer un pourcentage d’évolution, connaissant les pourcentages successivement appliqués, on calcule le produit des coefficients multiplicatifs associés. Il suffit

ensuite d’égaler le résultat obtenu avec et de résoudre cette équation d’inconnue t.

6. Comment analyser les variations d’un pourcentage ?

On sait que le pourcentage t est le résultat du calcul . Dans le tableau croisé suivant, on présente conjointement les variations du numérateur et du dénominateur en fonction de celles du pourcentage t.

Par exemple, si le nombre N d’élèves dans une classe augmente et que le nombre n de filles reste constant, alors le pourcentage t de filles dans la classe va diminuer.

À retenir absolument

Augmenter une quantité de t % revient à la multiplier par le coefficient multiplicatif .

De même, le coefficient multiplicatif associé à une baisse de t % est .

Lorsqu’une grandeur passe d’une valeur x0 à une valeur x1, le pourcentage t d’évolution est

donné par la relation : .

Lorsque t est suffisamment petit, n augmentations successives de t % donnent

approximativement le même résultat qu’une multiplication par .