Pourcentages (1re)

C’est sous la Révolution française que s’impose l’usage, dans notre pays, du système métrique décimal. On voit alors apparaître l’expression pour centqui au milieu du xixe siècle donne naissance au mot pourcentage.

La notion de pourcentage, utilisée aujourd’hui de manière quasi quotidienne dans la presse ou la publicité, est souvent mal maîtrisée et source d’erreurs. Précisons ici le calcul et l’usage des pourcentages.

1. Comment calculer un pourcentage ?

On définit d’abord E l’ensemble (ou la quantité) de référence, puis A la partie (ou la quantité) dont on calcule la proportion. On appelle, ici, n la grandeur de E et p la grandeur de A.
Le pourcentage de A dans E (ou de A par rapport à E) est le nombre t tel que :

 , soit .

Exemple

Sur une facture, on a les indications suivantes :

Prix HT : 250 € ; TVA : 45 € ; Prix TTC : 295 €.

Quel est le taux de TVA appliqué ?

On cherche le pourcentage de 45 par rapport à 250.

La quantité de référence est le prix HT : 250.

La quantité dont on calcule la proportion est : 45.

Le pourcentage de TVA est donc : . Soit 18 %.

2. Comment utiliser un pourcentage ?

Prendre t % d’un nombre x, c’est multiplier x par .

Ainsi, si un prix HT est de 330 € et que le taux de TVA est de 5,5 %, le montant de la TVA est

« 5,5 % de 330 », c’est-à-dire :  ; soit 18,15 €.

Si le nombre y représente t % de x, on a .

Prenons un exemple. La TVA sur un produit est de 6 % et s’élève à 27 €. Le prix hors taxe est le nombre x dont 6 % est égal à 27, c’est-à-dire le nombre x qui vérifie :

.

D’où .

Pourcentage de pourcentage : prendre m % de t % c’est prendre %.

Prenons un exemple. Dans un lycée, il y a 60 % de filles et parmi elles 30 % sont internes.

Le pourcentage de filles internes dans le lycée est : . Il y a donc 18 % de filles internes dans le lycée.

3. Comment calculer une augmentation ou une diminution de pourcentage ?

Augmenter une quantité de t % équivaut à multiplier sa valeur initiale par .

Ainsi, augmenter une quantité de 55 % équivaut à multiplier sa valeur initiale par

.

Diminuer une quantité de t % équivaut à multiplier sa valeur initiale par .

Ainsi, diminuer une quantité de 66 % équivaut à multiplier sa valeur initiale par

.

Remarque

Considérer une augmentation ou une diminution en pourcentage comme une multiplication par

facilite la résolution de nombreux problèmes. Il faut être capable d’utiliser ce résultat dans les deux sens :

• pour appliquer une augmentation ou une diminution (voir ci-dessus) ;

• pour déterminer un pourcentage d’augmentation ou de diminution.

Prenons un exemple. Le prix HT d’un produit est de 330 €, son prix TTC de 387,75 €. Pour trouver le taux de TVA (pourcentage d’augmentation), on appelle x une augmentation telle que :

.

Comme  , on en déduit que le taux de TVA est de 17,5 %.

4. Quel calcul effectuer dans le cas d’augmentations ou de diminutions successives ?

Appliquer à une quantité une augmentation de t % puis de m % équivaut à multiplier sa

valeur initiale par .

Appliquer à une quantité une diminution de t % puis de m % équivaut à multiplier sa valeur

initiale par .

Appliquer à une quantité une augmentation de t % puis une diminution de m % équivaut à

multiplier sa valeur initiale par .

5. Comment formuler des variations sous forme d’indices ?

On part d’une série chronologique :

L’indice à la date tk, en prenant 100 pour base à la date t0 , est la quantité :

.

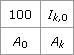
Remarques

L’indice est la quatrième proportionnelle dans le tableau de proportionnalité :

Les indices permettent non seulement de comparer plusieurs séries, mais aussi de déterminer rapidement des pourcentages d’évolution. Ainsi le pourcentage d’évolution de A0 à Ak est : %.

À retenir absolument
Le pourcentage de A de grandeur p dans E de grandeur n est le nombre .

Augmenter une quantité de t % équivaut à multiplier sa valeur initiale par : .

Diminuer une quantité de t % équivaut à multiplier sa valeur initiale par : .

L’indice Ik,0 à la date tk, en prenant 100 pour base à la date t0, est la quantité :

.