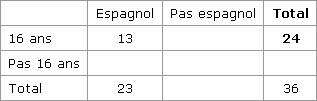
Outils graphiques de dénombrement

On étudie simultanément deux caractères A et B sur une population. On est alors amené à se poser différentes questions : « Combien d'individus vérifient le caractère A et le caractère B ? » « Combien ne vérifient que le caractère A ? » « Combien ne possèdent aucun de ces caractères ? » Pour résoudre ces problèmes de dénombrement, on peut représenter les données sous forme de tableau, de diagramme ou d'arbre.

1. Comment dénombrer à l'aide d'un tableau ?

Quand on étudie simultanément deux caractères sur une population et qu'à chaque caractère correspond un couple de valeurs, on peut présenter les résultats du dénombrement sous forme de tableau à double entrée (on parle aussi de tableau croisé).

Exemple

Dans une classe de 36 élèves : 24 élèves ont 16 ans ; 23 élèves font de l'espagnol ; 13 élèves ont 16 ans et font de l'espagnol. Nous pouvons dresser le tableau suivant.

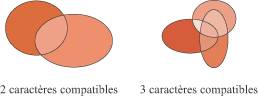
Grâce à ce tableau, nous pouvons facilement apporter une réponse aux questions du type : « Quelle est la répartition en âge des élèves qui ne font pas d'espagnol ? » ou encore « Combien d'élèves n'ont pas 16 ans et ne font pas d'espagnol ? ».

2. Comment dénombrer à l'aide d'un diagramme ?

Pour présenter les résultats d'un dénombrement, on peut également faire appel à un diagramme composé d'ensembles circulaires, chaque ensemble correspondant à un des caractères étudiés. Lorsque ces caractères sont incompatibles, les ensembles correspondants n'ont pas d'intersection.

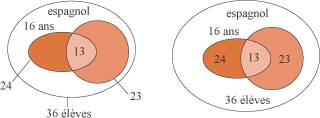
Attention, il faut noter convenablement les données sur le diagramme. Le premier diagramme ci-dessous correspond bien à l'exemple développé dans la question précédente, tandis que le second est incohérent. En effet, on y lit que 24 élèves ont 16 ans et ne font pas d'espagnol, que 23 élèves n'ont pas 16 ans et font de l'espagnol, et que 13 élèves vérifient les deux caractères à la fois ; selon ce diagramme, la classe comprendrait donc 60 élèves au lieu de 36.

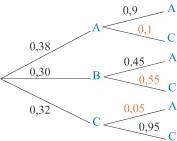
3. Comment dénombrer à l'aide d'un arbre pondéré ?

Lorsqu'au cours d'une étude, on a une succession de choix, on représente les différentes possibilités à l'aide d'un arbre. Il se peut que chaque choix soit pondéré ; les branches de l'arbre portent alors des coefficients et l'arbre est dit pondéré. C'est souvent le cas lorsque l'information est donnée sous forme de pourcentages.

Exemple

Trois candidats A, B et C se présentent à une élection. Au premier tour, 38 % des suffrages exprimés se portent sur le candidat A, 30 % sur le candidat B et 32 % sur le candidat C. Au second tour, deux candidats sont sélectionnés : A et C.

On sait que 90 % des personnes qui ont voté pour A au premier tour ont aussi voté pour A au second tour. De plus, 45 % des électeurs de B ont voté A. Enfin, 95 % des électeurs de C ont voté C au second tour.

À l'aide de ces données, on a construit et complété l'arbre pondéré suivant :

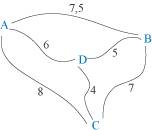
On peut en déduire que 34,2 % des électeurs ont voté A au premier et au second tour. En effet,  ; c'est ce que l'on appelle le « principe multiplicatif ». Remarquons que, dans un arbre pondéré, la somme des coefficients issus d'un même nœud vaut 1. C'est la « loi des nœuds ».

4. Comment dénombrer à l'aide d'un arbre de choix ?

On vient de voir que, lorsque plusieurs choix se succèdent, on peut représenter les différentes possibilités à l'aide d'un arbre.

Si l'on souhaite dénombrer toutes les possibilités, on dresse un arbre de choix.

Exemple

Un coursier doit livrer trois colis chez les clients A, B et C. On connaît la longueur de chaque trajet. On sait par ailleurs qu'il ne repasse pas par son point de départ D.

La carte donne les informations suivantes.

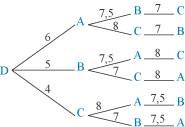
En dressant l'arbre de choix ci-dessous, il est ensuite facile de déterminer le trajet le plus court et le trajet le plus long.

À retenir absolument

Dans un exercice de dénombrement, il faut choisir le mode de représentation des données le plus adéquat.

Lorsque l'information est donnée sous la forme de pourcentages ou de pourcentages de pourcentages, on dresse un arbre pondéré. Il est alors nécessaire de connaître la « loi des nœuds » : la somme des coefficients affectés aux branches issues d'un même nœud vaut 1 ou 100 %. Il faut également savoir utiliser le « principe multiplicatif » : le coefficient affecté à un chemin est égal au produit des coefficients des branches qui le composent.