Opérations sur les fonctions (1re)

Les opérations sur les fonctions (somme, produit, quotient, valeur absolue, etc.) sont définies à partir des opérations déjà connues dans l’ensemble des nombres réels. Ce n’est pas le cas de la composition qui est liée à la notion même de fonction ; dans ce cas, il faut déterminer la fonction qui résulte de l’application successive de deux fonctions. On retrouve cette notion de composition en géométrie avec les transformations du plan.

1. Comment définir une fonction somme, une fonction produit, une fonction quotient, une fonction valeur absolue ?

Si les fonctions f et g sont définies sur un ensemble D et si k est un réel donné, alors les fonctions , , et sont définies pour tout réel x de D par :

 ;

 ;

 ;

.

Si de plus g ne s’annule pas sur D, alors la fonction est définie pour tout réel x de D par : .

Si l’ensemble D n’est pas précisé, il faut le rechercher. On utilise pour cela les résultats suivants :

 ;

 ;

est définie en tout point de où g ne s’annule pas.

2. Comment définir une fonction composée ?

Soit f une fonction définie sur un ensemble quelconque et g une fonction définie sur un ensemble tel que, pour tout , . On peut alors définir la fonction « composée de f suivie de g », notée et définie sur par .

Pour déterminer le domaine de la composée , on impose que : .

Remarque

Attention, en général .

3. Comment décomposer une fonction à l’aide des fonctions de référence ?

Pour décomposer une fonction f, il suffit de préciser les actions successives à effectuer pour transformer x en . On peut décrire chaque action à réaliser en français en utilisant un verbe à l’infinitif.

Exemple

Si la fonction f est définie sur par , alors les actions successives à effectuer sont les suivantes : à partir de x, retrancher 2, élever au carré, prendre l’inverse, multiplier par -5 et ajouter 2.

Ainsi, on peut décomposer f de la façon suivante : , avec

et .

4. Comment représenter f + k, kf et | f |, (où k est un réel)

Soit k un réel et Cf la courbe représentative, dans un repère du plan, d’une fonction f donnée.

La courbe représentative de la fonction est l’image de Cf par la translation de vecteur .

La courbe représentative de la fonction kf, est l’ensemble des points de coordonnées (x ; kf (x)) obtenu lorsque x décrit l’ensemble de définition de f.

Pour une abscisse x fixée, le point de la courbe représentative de kf a une ordonnée qui s’obtient en multipliant par k l’ordonnée du point de la courbe Cf.

La courbe représentative de la fonction est confondue avec Cf sur tout intervalle où f est positive. Sur tous les intervalles où f est négative, elle est l’image de Cf par la symétrie qui a pour axe l’axe des abscisses.

En effet, par définition de la valeur absolue on a :

• si , alors  ;

• si , alors .

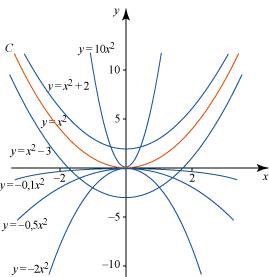
Exemples

Le graphique ci-dessous montre des courbes représentatives de fonctions liées à la fonction carré dont la courbe représentative est note C (courbe en orange).

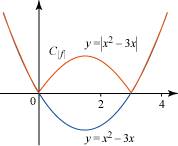
Le graphique ci-dessous montre la courbe représentative de la fonction où pour tout . La courbe de est en orange, les courbes de f et de coïncident sur les intervalles et .

À retenir absolument

est la fonction qui, à x, associe . On définit de la même façon les fonctions produit, quotient et valeur absolue.

La fonction composée est la fonction qui, à x, associe  ; l’ensemble de définition de est caractérisé par :

si et seulement si .

Les fonctions kf, , et , avec , ont le même ensemble de définition que f. Les

fonctions , fg et sont définies là ou f et g sont simultanément définies, en excluant de plus, pour le quotient, les zéros du dénominateur g.

La courbe représentative de la fonction , où , est l’image de la courbe représentative de la fonction f par la translation de vecteur .

La courbe représentative de la fonction est confondue avec celle de f pour les valeurs de x telles que . Elle est l’image de celle de f par la symétrie axiale d’axe (Ox) pour les valeurs de x telles que .