Opérations sur les fonctions (1re)

On effectue des opérations sur les fonctions de la même manière que l'on effectue des opérations sur les nombres : pour deux fonctions données, on peut définir leur somme, leur différence, leur produit, etc.

Il existe une opération propre aux fonctions : la composition. Composer deux fonctions c'est les enchaîner l'une derrière l'autre. Si l'on connaît les sens de variation de deux fonctions données, on peut en déduire le sens de variation de leurs composées.

Deux cas particuliers sont importants à connaître : la composition par une fonction constante et la composition par la fonction valeur absolue.

1. Comment définit-on la somme, la différence, le produit ou le quotient de deux fonctions données ?

Si f est une fonction définie sur un intervalle I et g une fonction définie sur un intervalle J, alors la fonction somme de f et g notée , la fonction différence , la fonction produit sont définies sur l'intervalle (intersection des intervalles I et J) respectivement par :

(f + g)(x) = f(x) + g(x) ;

 ;

 .

La fonction quotient est définie par , sur l'intervalle privé des valeurs pour lesquelles la fonction g s'annule.

2. Qu'est-ce que la composée de deux fonctions ?

Soit une fonction f définie sur un intervalle I et une fonction g définie sur un intervalle J. La composée de la fonction f suivie de la fonction g est une fonction u, définie pour tout x de I tel que , par  . Cette fonction est notée  ; on a alors : .

Remarque

La fonction composée de la fonction f suivie de la fonction g est généralement différente de la composée de g suivie de la fonction f. Dans la plupart des cas, on a : .

(Il suffit que pour une valeur x on ait : .)

3. Comment décomposer une fonction en une suite d'opérateurs ?

Les opérateurs les plus courants sont les fonctions suivantes :

• multiplier par un réel k :  ;

• ajouter un réel k :  ;

• prendre l'opposé :  ;

• prendre l'inverse :  ;

• élever au carré :  ;

• prendre la racine carrée :  ;

• soustraire un réel k :  .

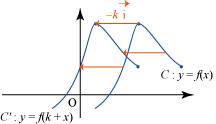
Pour décomposer une fonction, on cherche l'enchaînement des opérations à effectuer pour trouver l'image d'un nombre. À chaque opération on associe l'opérateur correspondant.

Exemple

Ainsi, pour calculer l'image d'un nombre par la fonction  , on doit soustraire 3 à x, puis élever le résultat au carré. C'est-à-dire appliquer successivement les deux opérateurs : et  .

On écrit alors : .

Ou encore : .

4. Comment déduire la représentation graphique des composées de la fonction f et de la fonction « ajouter un réel k » de la représentation graphique de la fonction f ?

Dans le repère ( ), la courbe représentant la fonction se déduit de la représentation graphique de la fonction f par la translation de vecteur .

Dans le repère ( ), la courbe représentant la fonction se déduit de la représentation graphique de la fonction f par la translation de vecteur .

5. Comment déduire la représentation graphique des composées de la fonction f et de la fonction « valeur absolue » de la représentation graphique de f ?

Soit (C) la courbe représentative de la fonction f.

La courbe représentant la fonction coïncide avec (C) lorsque (C) est au-dessus de l'axe des abscisses.

Elle est symétrique de (C) par rapport à l'axe des abscisses sur les intervalles où (C) est au-dessous de l'axe des abscisses.

La courbe représentant coïncide avec (C) lorsque (C) est à droite de l'axe des ordonnées, c'est-à-dire pour .

La courbe représentant , à gauche de l'axe des ordonnées (pour ), se déduit de (C) par symétrie par rapport à l'axe des ordonnées.

À retenir absolument

On définit la fonction somme, produit, différence ou quotient de deux fonctions comme la fonction qui à x associe la somme, le produit, la différence ou le quotient des images de x par chacune des fonctions.

On ne confondra pas l'image par la fonction produit , égale au produit des images par f et g et l'image par la fonction composée , égale à l'image par f de l'image par g. Pour la fonction produit, l'ordre d'utilisation des fonctions n'a pas d'importance, ce n'est pas le cas en général pour la fonction composée.

On déduit la représentation graphique des fonctions et de celle de f, par translation de vecteurs respectivement et .

On déduit la représentation graphique des fonctions et de celle de f, par symétrie par rapport respectivement à l'axe des abscisses et à l'axe des ordonnées.