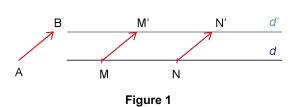
Observer les propriétés de conservation d'une translation

Si l'on construit l'image d'une figure par translation, on remarque que les deux figures ont la même forme et qu'elles sont disposées de la même façon.

Quelles propriétés de la translation peut-on en déduire ?

1. Image des figures de base

Soit A et B deux points distincts. On considère la translation transformant A en B.

L'image d'une droite est une droite qui lui est parallèle.

L'image d'une demi-droite est une demi-droite qui lui est parallèle et de même sens.

L'image d'un segment [MN] est un segment [M'N'] tel que MNN'M' est un parallélogramme.

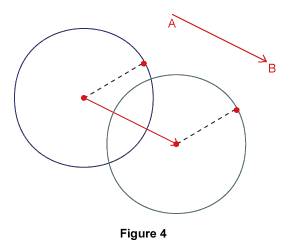
L'image d'un cercle est un cercle ayant le même rayon.

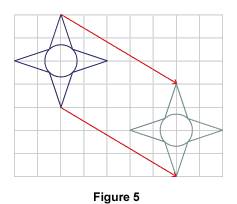
Ces propriétés permettent de construire l'image des figures de base. Par exemple, pour construire l'image d'un cercle, il suffit de construire l'image du centre et de tracer le cercle centré en cette image et de même rayon que le cercle initial.

2. Propriétés conservées par une translation

Sur le schéma suivant, la figure verte est l'image de la figure bleue par translation. Les deux figures sont superposables.

On peut en conclure qu'une translation conserve :

l'alignement ;

les longueurs ;

les angles. En particulier deux droites perpendiculaires ont pour images deux droites perpendiculaires ;

le milieu d'un segment ;

les aires.