|
||||||
| Institut THOMASTA : Quelles seront les nouvelles technologies de demain ? | ||||||
|
||||||
|
||||||
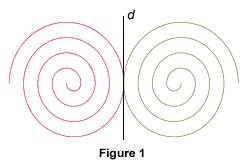
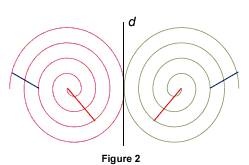
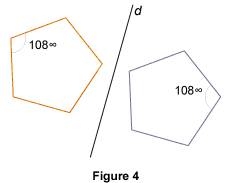
Observer les propriétés de conservation d'une symétrie axiale
|
||||||
|
Prof.: Thomas TAMENOU - Thomasta.com -
Contactez-nous |
||||||
 |