Nombre dérivé et fonction dérivée

Le concept de dérivée n'a été dégagé qu'il y a environ trois siècles. Il est lié, en mathématiques, à la notion de tangente à une courbe, et en sciences physiques, à celle de vitesse instantanée d'un mobile. Les calculs de dérivées ont de nombreuses applications : ils permettent de déterminer les variations d'une fonction, de résoudre des problèmes d'optimisation, de calculer certaines limites, etc.

1. Comment définir le nombre dérivé d'une fonction en un réel ?

Soit f une fonction définie sur un intervalle I ouvert et a un réel appartenant à I.

On dit que f est dérivable en a si le taux d'accroissement de f en a admet une limite finie quand x tend vers a. Dans ce cas, ce réel est appelé le nombre dérivé de f en a et est noté  :

.

2. Que représente le nombre dérivé d'une fonction en un réel ?

Lorsqu'une fonction f est dérivable en un réel a d'un intervalle ouvert I, le nombre dérivé de f en a, , est le coefficient directeur de la tangente à C, la courbe représentative de f, au point d'abscisse a de C.

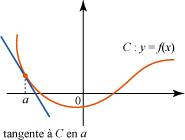
3. Quelle est l'équation de la tangente à la courbe d'une fonction, en un point ?

Soit f une fonction définie sur un intervalle ouvert I, dérivable en un réel a de I. On note T la tangente à la courbe représentative de f au point d'abscisse a.

Par définition, T est une droite de coefficient directeur . De plus, T passe par le point .

En traduisant ces deux conditions, on obtient l'équation de T : .

4. Qu'est-ce que l'approximation affine d'une fonction dérivable en un point ?

Soit f une fonction définie sur un intervalle ouvert I et dérivable en un réel a de I. La fonction est appelée l'approximation affine de f en a.

Ainsi, localement en a, si l'on remplace f par son approximation affine en a, on commet une erreur très faible. Ce qui s'écrit aussi : si x est voisin de a, .

5. Qu'est-ce que la fonction dérivée d'une fonction dérivable sur un intervalle ?

Soit f une fonction définie sur un intervalle ouvert I.

On dit que f est dérivable sur I lorsque f est dérivable en tout réel x de I.

Soit f une fonction définie et dérivable sur un intervalle I.

La fonction qui, à tout réel x de I, associe le nombre dérivé est appelée la fonction dérivée de f sur I. Elle est notée f'.

À retenir absolument

Une fonction f, définie sur un intervalle ouvert contenant un réel a, est dérivable en a si admet une limite finie lorsque x tend vers a. Ce réel est alors noté et appelé le « nombre dérivé de f en a ».

Dans ce cas, est le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse a. Cette tangente a alors pour équation .

Si une fonction f est définie et dérivable en tout réel x d'un intervalle ouvert I, alors la fonction qui, à tout , associe est la fonction dérivée de f sur I, elle est notée f'.