Nature et écriture des nombres

« Le nombre entier vient de Dieu. Tout le reste est l’œuvre de l’homme. » Leopold Kronecker (1823-1891).

Les entiers naturels ont été considérés à certaines époques comme une connaissance innée ou comme un don des dieux. Depuis, d’autres familles de nombres ont été « construites » pour résoudre de nouveaux problèmes : nombres décimaux pour améliorer les techniques opératoires, nombres relatifs pour tenir compte des échanges commerciaux, nombres rationnels et irrationnels pour mesurer des grandeurs, etc.

Nous allons étudier ici ces différents ensembles de nombres.

1. Comment déterminer à quel(s) ensemble(s) appartient un nombre ?

On distingue plusieurs ensembles de nombres.

est l’ensemble des nombres entiers ou entiers naturels.

 =  .

est l’ensemble des nombres entiers relatifs.

 =  .

est l’ensemble des nombres décimaux. Ce sont les nombres qui peuvent s’écrire sous la

forme avec et  ; ces nombres ont un nombre fini de chiffres après la virgule.

Par exemple : est un décimal, mais n’est pas un décimal.

est l’ensemble des nombres rationnels. Ce sont les nombres qui peuvent s’écrire sous la

forme avec et * (ce sont donc des quotients d’entiers).

Par exemple : et sont des rationnels, mais n’est pas un rationnel.

est l’ensemble des nombres réels. C’est l’ensemble de tous les nombres que nous utilisons ; on peut le représenter par une droite graduée :

Chaque nombre réel est représenté par un point et chaque point représente un réel.
Cet ensemble comprend des nombres irrationnels, c’est-à-dire des nombres réels qui ne sont pas rationnels.

Ces ensembles de nombres vérifient les inclusions :                 .

Ce qui signifie qu’un naturel est aussi un entier relatif, qu’un entier relatif est aussi un décimal, etc.

Pour reconnaître la nature d’un nombre :

on simplifie au maximum son écriture ;

dans le cas d’un quotient irréductible , on effectue la division. Si elle se termine (si le reste

est nul), est un décimal ; si elle ne se termine pas, on obtient une écriture périodique et est un rationnel qui n’est pas un décimal ;

si on ne peut pas écrire le nombre comme un quotient d’entiers, alors c’est un irrationnel.

2. Comment écrire un nombre décimal ?

Dans les matières scientifiques, on utilise souvent, pour écrire un nombre décimal, les puissances de 10, de façon à avoir immédiatement une idée de l’ordre de grandeur de celui-ci.

Exemple

Soit le décimal 28 642,357.

On peut l’écrire avec un entier et une puissance de 10 : .

L’écriture scientifique de ce nombre est l’écriture composée d’un décimal compris entre 1 et 10, 10 exclu, et d’une puissance de 10 : .

En arrondissant le décimal de l’écriture scientifique à l’entier le plus proche, on obtient un ordre de grandeur du nombre : .

3. Comment déterminer une valeur approchée ?

Lorsque l’on veut écrire un nombre réel dans le système décimal et que celui-ci n’est pas un nombre décimal, on doit utiliser une valeur approchée.

Par exemple, . Il n’y a pas égalité car les « 3 » continuent à l’infini.

Une valeur approchée peut être définie par défaut ou par excès. On parle de valeur approchée à près, où p est un entier, quand la différence entre le nombre et sa valeur approchée est inférieure à .

Pour déterminer la valeur approchée d’un nombre réel positif à n décimales :

• par défaut, on effectue la troncature à n décimales de ce nombre (cela revient à supprimer les décimales qui suivent les n premières décimales) ;

• par excès, on prend la valeur approchée par défaut et on ajoute 1 à la dernière décimale (cela revient à ajouter à la valeur approchée par défaut) ;

Pour déterminer la valeur approchée d’un nombre réel négatif à n décimales :

• par excès, on effectue la troncature à n décimales de ce nombre ;

• par défaut, on prend la valeur approchée par excès et on ajoute 1 à la dernière décimale.

Pour calculer l’arrondi d’un nombre réel à n décimales, on considère la troncature du nombre à n décimales, puis :

• si la -ième décimale est 0, 1, 2, 3 ou 4, alors l’arrondi est la troncature ;

• si la -ième décimale du nombre réel est 5, 6, 7, 8 ou 9, alors on obtient l’arrondi en ajoutant 1 à la dernière décimale de la troncature.

4. Comment savoir si un entier est ou n’est pas divisible ?

On dit qu’un entier b divise un entier a lorsqu’il existe un entier q tel que

On dit alors que b est un diviseur de a et que a est un multiple de b.

Pour trouver certains diviseurs, il suffit de connaître quelques critères de divisibilité :

• un entier est divisible par 2 si son dernier chiffre est 0, 2, 4, 6 ou 8 ;

• un entier est divisible par 3 si la somme de ses chiffres est multiple de 3 ;

• un entier est divisible par 4 si le nombre constitué de ses deux derniers chiffres est divisible par 4 ;

• un entier est divisible par 5 si son dernier chiffre est 0 ou 5 ;

• un entier est divisible par 9 si la somme de ses chiffres est multiple de 9 ;

• un entier est divisible par 10 si son dernier chiffre est 0.

Un nombre premier est un entier naturel n’ayant que deux diviseurs distincts : 1 et lui-même.

Il est important de connaître les plus petits nombres premiers (on les obtient à l’aide du crible d’Ératosthène). Ce sont les nombres : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,...

Pour chercher si un nombre est premier :

• on vérifie d’abord que les critères de divisibilité ne s’appliquent pas ;

• puis on divise ce nombre par les nombres premiers 7, 11, 13, 17,... À chaque fois, on vérifie que le reste de la division est non nul (la division « ne tombe pas juste »). Quand le quotient devient inférieur au diviseur, il est inutile d’aller plus loin.

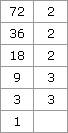
5. Comment et pourquoi décomposer un nombre en facteurs premiers?

252 n’est pas premier. En effet . Ainsi le nombre 252 est égal à un produit de nombres premiers. Plus généralement, on peut dire que tout nombre entier supérieur ou égal à 2 est premier ou produit de nombres premiers.

Lorsqu’on décompose un entier sous la forme d’un produit de nombres premiers, on dit qu’on décompose ce nombre en facteurs premiers.

Pour décomposer un nombre en facteurs premiers, par exemple 72, on peut :

• soit utiliser les tables de multiplication :  ;

• soit diviser successivement par les nombres premiers : 2, 3, 5, 7, etc. On obtient, pour notre exemple, le tableau ci-dessous :

On en déduit que .

On utilise la décomposition en facteurs premiers pour simplifier les écritures de quantités écrites avec des fractions et des radicaux. On l’utilise aussi pour déterminer le plus grand diviseur d’un ensemble de nombres ou leur plus petit multiple commun.

À retenir absolument

                .

Écrire un nombre décimal en écriture scientifique, c’est l’écrire comme produit d’un décimal compris entre 1 et 10, 10 exclu, et d’une puissance de 10.

Un nombre premier est un entier naturel n’ayant que deux diviseurs distincts : 1 et lui-même.