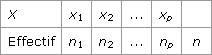
Mesures de dispersion d'une série

Une étude statistique se déroule normalement de la manière suivante :

1. classement des données en un tableau : c’est le tableau de la série statistique ;

2. représentation graphique de cette série ;

3. caractérisation de la série à l’aide de paramètres, afin, par exemple, de la comparer à d’autres séries statistiques.

Deux paramètres dits de position (la moyenne et la médiane) ont été étudiés en seconde. Sont définis ici de nouveaux paramètres dits de dispersion : les quartiles, la variance, l’écart-type et l’intervalle interquartile, ainsi qu’un nouveau type de représentation graphique, le diagramme en boîte, qui permet de comparer rapidement deux séries.

1. Comment calculer une variance et un écart-type ?

Soit la série statistique de taille n suivante :

On remarque que  .

On rappelle que la moyenne de X est le nombre :

.

On appelle variance de la série statistique X le nombre :

.

Ce que l’on écrit de manière plus compacte : .

L’écart-type de X est le nombre .

Remarques

La variance et l’écart-type mesurent la façon dont les valeurs de X se dispersent autour de la moyenne. Ce sont des paramètres de dispersion (alors que la moyenne et la médiane sont des paramètres de position : ils précisent vers quelles valeurs se situe la série).

On peut aussi calculer la variance à l’aide de la formule suivante :

.

Dans le cas où, au lieu d’avoir une valeur xi, on a un intervalle, on utilise les mêmes formules dans lesquelles on remplace xi par le centre de l’intervalle.

2. Comment calculer la médiane d’une série statistique ?

La médiane, notée me, est le nombre qui sépare la série ordonnée en deux groupes de même effectif.

Pour la déterminer, on écrit la liste de toutes les valeurs de la série par ordre croissant, chacune d’elle répétée autant de fois que son effectif.
Si l’effectif total n est un nombre impair, la médiane est le terme de rang .

Si l’effectif total n est un nombre pair, la médiane est le centre de l’intervalle formé par les termes de rang et .

Remarque

Quand la série est regroupée par classes, on détermine la médiane graphiquement à partir de la courbe des effectifs cumulés ou de celle des fréquences cumulées.

3. Comment déterminer les quartiles d’une série statistique ?

Soit une série statistique X de taille n.

Le premier quartile Q1 est la plus petite valeur de la série telle qu’au moins 25 % des données soient inférieures ou égales à Q1.

Le troisième quartile Q3 est la plus petite valeur de la série telle qu’au moins 75 % des données soient inférieures ou égales à Q3.

L’intervalle interquartile est l’intervalle .

Le nombre s’appelle l’interquartile.

Pour déterminer les quartiles Q1 et Q3, on procède un peu comme pour la médiane. On écrit la liste de toutes les valeurs de la série par ordre croissant, chacune d’elle répétée autant de fois que son effectif.

Si est un entier p, Q1 est le terme de rang p et Q3 est le terme de rang 3p ;

Si n’est pas un entier, Q1 est le terme de rang immédiatement supérieur à et Q3 est le

terme de rang immédiatement supérieur à .

Remarque

Quand la série est regroupée par classes, on détermine les quartiles graphiquement à partir de la courbe des effectifs ou des fréquences cumulés.

4. Comment se transforment les paramètres d’une série lors d’un changement affine ?

Soit la série statistique X de taille n suivante :

On considère la série statistique . C’est-à-dire la série :

où .

En reprenant les notations précédentes, on a :

, et .

Si sont respectivement la médiane, le 1er quartile et le 3e quartile de X et, si

sont la médiane, le 1er quartile et le 3e quartile de Y, alors on a :

.

Et, si , alors et .

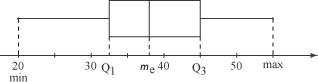
Mais, si a < 0, alors et .

5. Comment tracer un diagramme en boîte ?

On construit un diagramme en boîte de la façon suivante :

• sur un axe vertical ou horizontal, on repère les valeurs de la série statistique ;

• on place le minimum et le maximum de la série, le 1er quartile, le 3e quartile et la médiane ;

• on construit le rectangle (la boîte) parallèle à l’axe, de longueur égale à l’interquartile et de largeur arbitraire.

Ce diagramme en boîte est aussi appelé diagramme à moustaches ou diagramme à pattes.

Exemple

Soit une variable statistique X dont le maximum est 55, le minimum 20, la médiane 38, le 1er quartile 32,5 et le 3e quartile 45. On construit alors le diagramme en boîte suivant :

À retenir absolument

Soit X une série statistique.

La variance de X est .

L’écart-type de X est le nombre .

Le premier quartile de X, noté Q1, est la plus petite valeur de la série telle qu’au moins 25 % des données soient inférieures ou égales à Q1.

Le troisième quartile de X, noté Q3, est la plus petite valeur de la série telle qu’au moins 75 % des données soient inférieures ou égales à Q3.

L’intervalle interquartile est l’intervalle .