Fonction logarithme népérien

La fonction logarithme népérien est très utile pour simplifier certaines expressions mathématiques. Elle permet de convertir une multiplication en addition, une division en soustraction, une puissance en multiplication, une racine en division. Elle offre également la possibilité de résoudre les équations dont l’inconnue figure en exposant.

1. Quelles sont les caractéristiques de la fonction logarithme népérien ?

La fonction logarithme népérien est la primitive de la fonction Son ensemble de définition s’étend sur ]0 ; + [.

On retiendra deux valeurs remarquables : .

La dérivée de la fonction logarithme népérien étant strictement positive, cette fonction est donc strictement croissante sur ]0 ; + [.

Donc, pour deux nombres a et b strictement positifs :

ln a = ln b équivaut à a = b (deux nombres qui ont le même logarithme sont égaux) ;

ln a < ln b équivaut à a < b (le logarithme conserve l’ordre des nombres).

Comme la fonction logarithme népérien est strictement croissante et que ln 1 = 0 alors : ln x

 < 0 si  ; ln x > 0 si .

La représentation graphique de la fonction logarithme népérien passe, dans le repère

orthonormé , par les points remarquables (1 ; 0) et (e ; 1). On mémorisera la position de la courbe par rapport aux axes et à la droite d’équation y = x.

2. Quelles limites faut-il connaître ?

Au voisinage de 0 :

Lorsque x tend vers 0, la courbe s’approche de l’axe des ordonnées. L’axe des ordonnées est donc une asymptote verticale.

Au voisinage de +  :

Lorsque x tend vers l’infini, la courbe continue à s’élever puisque la fonction logarithme népérien est une fonction strictement croissante. Il n’y a donc pas d’asymptote horizontale.
Au voisinage de +  :

On remarque que la courbe d’équation y = ln x tend vers l’infini infiniment moins vite que la droite d’équation y = x.

Cette limite sera utile pour lever l’indétermination de la forme «   –   » au voisinage de l’infini. Il suffira alors de factoriser x pour faire apparaître un tel quotient.

3. Comment transformer le logarithme d’un produit, d’une puissance, d’un quotient ou d’une racine ?

Il faut retenir que : ln (a × b) = ln a + ln b. Le logarithme d’un produit est la somme des logarithmes de ses facteurs.

On en déduit que :

 ;

 ;

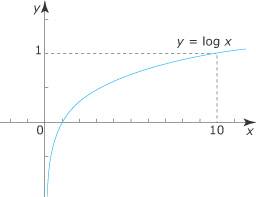
4. Quelles sont les primitives de la composée par une fonction logarithme ?

Si f est la composée d’une fonction u, suivie de la fonction logarithme népérien, c’est-à-dire si

, alors

Réciproquement, si une fonction se présente sous la forme , alors la famille de ses

primitives s’écrit (il faut prendre la valeur absolue car la fonction doit être strictement positive).

Ainsi, f définie sur par peut se noter

Une primitive de f sur cet intervalle est alors

5. Quelle est l’utilité de la touche « log » de la calculatrice ?

La touche « log » permet de calculer le logarithme décimal d’un nombre réel strictement

positif. La fonction logarithme décimal est définie sur ]0 ; + [ par la relation :

Par conséquent : .

Les propriétés de cette fonction sont identiques à celles de la fonction logarithme népérien. Les économistes préfèrent cependant le logarithme décimal car les grandeurs étudiées sont souvent des puissances de 10. L’exposant se retrouve facilement en utilisant la formule :

.

À retenir

La fonction logarithme népérien est la primitive de la fonction inverse qui prend la valeur 0 en 1.

Elle est définie sur ]0 ; + [ et est strictement croissante sur cet intervalle.

 ;  l’axe des ordonnées est donc une asymptote verticale de la courbe d’équation ln x.

Le logarithme d’un produit est la somme des logarithmes de ses facteurs.