 |
||||||
| Institut THOMASTA : Quelles seront les nouvelles technologies de demain ? | ||||||
|
||||||
|
||||||
Fonction exponentielle de base a On appelle fonction exponentielle de base a la fonction Elles sont aussi utilisées lorsque les points d'un nuage (x ; y) ne sont pas suffisamment alignés pour réaliser un ajustement affine. 1. Comment transforme-t-on une exponentielle de base a en une exponentielle de base e ? Pour a > 0, on sait que y = ax équivaut à ln y = ln ax = x ln a. Comme l'exponentielle de base e est une fonction strictement croissante, on en déduit : eln y = exln a, soit y = ex ln a. Donc y = ax équivaut à y = ex ln a. 2. Quel est le sens de variation des fonctions ax ? La fonction f définie sur Sachant que La fonction exponentielle étant strictement positive, la dérivée est du signe de ln a. Pour 0 < a < 1, ln a est négatif donc la fonction ax est décroissante. Pour a > 1, ln a est positif donc la fonction ax est croissante. Notons que, pour a = 1, la fonction ax est constante. On vérifie graphiquement les différents sens de variation en traçant les courbes d'équations y = 0,5x, y = 1x et y = 2x.
3. Quelles sont les limites de ax en –∞ et +∞ ? Pour 0 < a < 1, ln a est négatif. Donc au voisinage de – De même, au voisinage de + La courbe admet l'axe des abscisses pour asymptote au voisinage de + Pour a > 1, ln a est positif. Donc, au voisinage de La courbe admet l'axe des abscisses pour asymptote au voisinage de – De même, au voisinage de 4. Par quelles fonctions traduit-on une évolution à taux constant ? On sait qu'augmenter une quantité Q0 de t % sur une période revient à la multiplier par le coefficient multiplicateur (1 + t). Donc au bout de n périodes, la quantité obtenue sera : Qn = Q0(1 + t)n. De même, diminuer cette quantité de t % sur une période revient à la multiplier par (1 – t). Donc au bout de n périodes, la quantité obtenue sera : Qn = Q0(1 – t)n. Par exemple, pour calculer la valeur acquise au bout de 10 ans par un capital de 10 000 € placés à 5 % l'an à intérêts composés, on affiche sur la calculatrice : 10 000 × 1,0510. La valeur acquise est de 16 288,95 €. (Dans un placement à intérêts composés, les intérêts sur une période s'ajoutent au capital pour produire à leur tour des intérêts. On dit que l'on capitalise les intérêts.) 5. Qu'est-ce qu'un ajustement exponentiel ? Quand, dans une série statistique à deux variables, les points Dans ce cas, on en déduit une relation de la forme D'où : Soit plus simplement : À retenir L'égalité y = ax équivaut à y = ex ln a. La fonction f définie sur La fonction exponentielle étant strictement positive, le signe de la dérivée dépend du signe de ln a. Pour a > 1 :
Pour 0 < a < 1 :
|
||||||
|
Prof.: Thomas TAMENOU - Thomasta.com -
Contactez-nous |
||||||
 |

 d'où :
d'où :  d'où :
d'où : 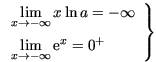 d'où :
d'où :  d'où :
d'où :