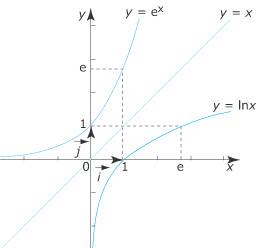
Fonction exponentielle (Terminale)

La fonction exponentielle de base e, notée ou , est une fonction de référence au programme de terminale. Ses propriétés se déduisent de celles de la fonction logarithme népérien, par simple symétrie. On doit aussi connaître sa dérivée et certaines formules qui relient l’exponentielle au logarithme.

1. Quelles sont les relations entre logarithme et exponentielle ?

Pour un exposant n entier ou fractionnaire, on sait que : ln an = n ln a.

Cette relation se généralise pour un exposant x réel : ln ex = x ln e = x.

Donc : ln ex = x.

Quand on applique cette formule, l’égalité y = eln x équivaut à ln y = ln eln x ou ln y = ln x × ln e = ln x. La fonction logarithme népérien étant strictement croissante, on en déduit que y = x. D’où : eln x = x.

2. Par quelle transformation passe-t-on du tracé de la fonction logarithme à celui de la fonction exponentielle ?

Les représentations graphiques des fonctions exponentielle et logarithme népérien sont,

dans le repère orthonormé , symétriques par rapport à la droite d’équation y = x. En effet, tout point M(x ; lnx) de la courbe d’équation y = lnx a pour symétrique le point M’(lnx ; x).

Comme elnx = x, M’ est un point de la représentation graphique de la fonction exponentielle.

En particulier, le point (e ; 1) sur la courbe de la fonction logarithme a pour symétrique le point (1 ; e) sur la courbe de la fonction exponentielle. De cette symétrie découlent toutes les propriétés de la fonction exponentielle. On retiendra deux valeurs remarquables : e0 = 1 et e1 = e.

La fonction ex est définie sur , strictement croissante et strictement positive (son tracé est toujours au-dessus de l’axe des abscisses).

3. Quelles sont les limites à connaître ?

Au voisinage de –  :

L’axe des ordonnées est asymptote verticale pour la courbe de ln x au voisinage de 0. Par la symétrie axiale, l’axe des abscisses devient une asymptote horizontale pour la courbe de ex au voisinage de – .

Au voisinage de +  :

Cette limite se déduit de par symétrie.

Au voisinage de +  :

On vérifie graphiquement que l’exponentielle s’élève vers l’infini, infiniment plus vite que la droite d’équation y = x.

4. Quelles sont la dérivée et les primitives de la fonction exponentielle ?

On sait que y = ex équivaut à ln y = x.

En dérivant y par rapport à x, on obtient : , soit : y’ = y.

Donc : (ex)’ = ex.

Plus généralement, si f est la composée d’une fonction u suivie de la fonction exponentielle, alors : f(x) = eu(x).

De la formule de la dérivée d’une fonction composée, on déduit : f’(x) = eu(x) × u’(x)

Soit (eu)’ = eu × u’.

Réciproquement, la fonction a pour famille de primitives  .

Une fonction de la forme a pour famille de primitives .

5. Comment transformer l’écriture d’une exponentielle ?

Pour deux exposants réels a et b, les propriétés sont les mêmes que pour l’élévation à une puissance entière.

En particulier, l’exponentielle de la somme est égale au produit des exponentielles de ses termes : .

De même, l’exponentielle de la différence est égale au quotient des exponentielles de ses

termes :

Pour élever une exponentielle à une puissance entière, on multiplie les exposants : .
Pour passer de l’écriture exponentielle à l’écriture sous forme de quotient, on peut appliquer la

relation :

À retenir

Les représentations graphiques de la fonction exponentielle de base e et de la fonction logarithme népérien sont symétriques par rapport à la droite d’équation y = x.

La fonction est strictement croissante et strictement positive sur .

 ;  l’axe des abscisses est donc une asymptote horizontale pour la courbe

d’équation .

La fonction est égale à sa propre dérivée.

L’exponentielle de la somme est égale au produit des exponentielles de ses termes. De même, l’exponentielle de la différence est égale au quotient des exponentielles de ses termes.