Équations de droite et systèmes d'équations linéaires

On doit à René Descartes (1596-1650), philosophe et mathématicien, la méthode qui consiste à remplacer un problème de géométrie par un problème numérique à l’aide d’équations dites cartésiennes.

Comment déterminer une équation de droite ? En quoi des équations de droite permettent-elles de résoudre des problèmes de parallélisme ou d’orthogonalité ? Voilà deux questions que l’on va être amené à se poser dans ce chapitre.

On verra par ailleurs qu’un système de deux équations à deux inconnues peut s’interpréter à l’aide d’équations de droites ; en effet, résoudre un tel système revient à chercher les coordonnées d’un point d’intersection de deux droites.

1. Comment déterminer une équation de droite ?

Soit A(xA ; yA) et B(xB ; yB) deux points donnés dans un repère, déterminer une équation de la droite (AB) consiste à chercher une condition qui soit nécessaire et suffisante pour qu’un point M(x ; y) soit aligné avec A et B : cette condition est la colinéarité des vecteurs et .

Le vecteur a pour coordonnées (xB - xA ; yB - yA), le vecteur a pour coordonnées (x - xA ; y - yA), la condition de colinéarité s’écrit alors :

(x - xA)(yB - yA) = (y - yA)(xB - xA).

On distingue deux cas :

• si les points A et B ont la même abscisse k, soit , l’équation de la droite (AB) est alors  ; cette droite est parallèle à l’axe des ordonnées ;

• si , on peut calculer le coefficient directeur de la droite (AB) : , et l’ordonnée à l’origine : . L’équation de la droite (AB) est alors : .

Réciproquement, dans un repère du plan, l’ensemble des points M de coordonnées (x ; y) tels que est une droite qui n’est pas parallèle à l’axe des ordonnées.

Exemple

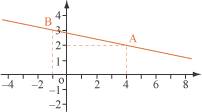
Soit les deux points A(4 ; 2) et B(-1 ; 3) et M un point quelconque de coordonnées (x ; y).

On calcule les coordonnées des vecteurs et , on obtient et .

On écrit alors que M est aligné avec A et B si et seulement si les « produits en croix » sont égaux, ce qui se traduit par l’équation , qui est l’équation de la droite (AB).

Après transformation de l’égalité, on obtient l’équation : .

2. Comment utiliser une équation de droite ?

Pour dire si un point est sur une droite : on remplace les inconnues de l’équation de la droite par les coordonnées du point et on vérifie si l’équation ainsi obtenue est vraie.

Par exemple, le point E de coordonnées (2 ; -1) est-il sur la droite d’équation  ?

Pour répondre, on remplace x par 2 dans la formule  ; si l’on trouve -1 le point est sur la droite, sinon il ne l’est pas.

Ici donc le point E est bien sur la droite.

Pour construire une droite, connaissant son équation, on distingue deux cas :

• si l’équation est de la forme x = k, la droite est parallèle à l’axe des ordonnées ; on place le point de coordonnées (k ; 0) et on trace la droite ;

• si l’équation est de la forme y = mx + p, on choisit deux valeurs distinctes x1 et x2 de x et on trace la droite qui passe par les points de coordonnées (x1 ; mx1 + p) et (x2 ; mx2 + p). On peut en particulier choisir x = 0 et , la droite passe donc par les points (0 ; p) et .

Exemple

On veut tracer la droite d’équation .

On choisit une valeur de x, par exemple 6 pour pouvoir diviser par 3, puis on calcule y :

. On obtient le point A de coordonnées (6 ; 2).

On recommence avec une autre valeur de x, par exemple -3 ; on calcule y et on obtient le point B de coordonnées (-3 ; 5).

Il reste à placer ces points et à tracer la droite.

3. Quels problèmes de géométrie peut-on résoudre à l’aide d’équations de droites ?

On peut démontrer que deux droites sont parallèles.

Deux droites d’équations respectives et sont parallèles si et seulement si elles ont le même coefficient directeur, c’est-à-dire si .

Par exemple, la droite d’équation et la droite d’équation sont parallèles car

on peut écrire et .

On peut déterminer l’équation réduite de la parallèle à une droite donnée passant par un point donné.

Par exemple, la parallèle à la droite d’équation passant par le point A(1 ; 4) a aussi le coefficient directeur 2. Son ordonnée à l’origine b est donnée par : . D’où l’équation cherchée : .

4. Comment déterminer par le calcul le point d’intersection de deux droites ?

Une équation d’une droite D peut s’écrire sous la forme avec a et b non simultanément nuls. Une telle équation s’appelle équation linéaire à deux inconnues. Les solutions de cette équation sont les coordonnées des points de la droite D.

Déterminer par le calcul les coordonnées du point d’intersection de deux droites revient à résoudre un système de deux équations linéaires à deux inconnues constitué des deux équations des deux droites. C’est un système de la forme : .

Résoudre un tel système, c’est trouver tous les couples qui sont solutions des deux équations en même temps. Si de tels couples existent, les points qu’ils repèrent appartiennent aux droites d’équations respectives et .

On distingue trois cas présentés dans le tableau ci-dessous :

Il existe deux méthodes pour résoudre algébriquement un système de deux équations linéaires à deux inconnues :

• la méthode par substitution, qui consiste à exprimer une des inconnues en fonction de l’autre dans une équation puis à remplacer cette inconnue par l’expression obtenue dans l’autre équation ;

• la méthode par combinaison, qui consiste à obtenir, en combinant les deux équations, une équation dans laquelle il n’y a plus qu’une inconnue. Cette équation étant résolue, on calcule l’autre inconnue en utilisant la valeur trouvée.

À retenir absolument

Si une droite est parallèle à l’axe des ordonnées, alors son équation est de la forme  : sinon son équation est de la forme , où m est son coefficient directeur et p son ordonnée à l’origine.

Deux droites sont parallèles si leurs coefficients directeurs sont égaux.

Deux droites sont perpendiculaires si le produit de leurs coefficients directeurs vaut -1.

Calculer les coordonnées du point d’intersection de deux droites revient à résoudre le système constitué des deux équations des droites en question.