Donner l'arrondi ou la troncature à l'unité

Pierre doit 5,6 euros à Jacques, mais il n'a sur lui que des pièces de 1 euro et Jacques n'a pas de quoi lui rendre la monnaie. Il décide de lui donner 6 euros, ce qui correspond à l'arrondi de 5,6 à l'unité.

Quelle règle permet de déterminer l'arrondi à l'unité d'un nombre décimal ? Et quelle est donc la différence entre arrondi et troncature à l'unité ?

1. Arrondi à l'unité

Exemple : sur la figure 1, on a placé les nombres 8 ; 8,36 ; 8,5 ; 8,74 et 9 sur un axe.

Comme 8,36 est plus près de 8 que de 9, l'arrondi à l'unité de 8,36 est le nombre 8.

Pour une raison analogue, l'arrondi à l'unité du nombre 8,74 est le nombre 9.

Pour le nombre 8,5, il faut faire un choix, car il est situé à la même distance de 8 et de 9. On a décidé de choisir 9 pour arrondi à l'unité de 8,5.

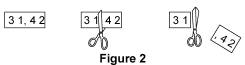
Définition : soit a un nombre décimal non entier :

dans le cas où la partie décimale de a est 0,5, l'arrondi à l'unité de a est l'entier immédiatement supérieur à a ;

dans les autres cas, l'arrondi à l'unité de a est le nombre entier le plus proche de a.

2. Troncature à l'unité

Exemple : les figures illustrent une façon d'obtenir la troncature à l'unité du nombre 31,42. Cette troncature est égale à 31. Il suffit de « découper la partie décimale » de l'écriture du nombre.

Définition : la troncature à l'unité d'un nombre décimal non entier d est le plus grand entier inférieur ou égal à d.

Il y a donc deux possibilités :

soit la troncature est égale à l'arrondi à l'unité (c'est le cas pour 8,36) ;
soit la troncature est égale à l'arrondi à l'unité diminué de 1 (c'est le cas pour 8,74).