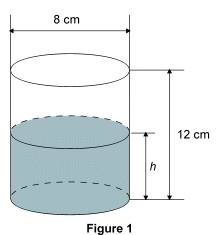
Déterminer une fonction linéaire

Quels sont les éléments dont on doit disposer pour déterminer une fonction linéaire, c'est-à-dire pour la connaître entièrement ?

1. Déterminer une fonction linéaire par le calcul

On sait qu'une fonction linéaire est une fonction du type , où a est un nombre fixé appelé coefficient de cette fonction. Par conséquent, pour déterminer une fonction linéaire, il suffit de trouver son coefficient.

1.1. On connaît l'image d'un nombre non nul donné

Exemple : on veut déterminer la fonction linéaire qui à 12 fait correspondre l'image 44, autrement dit la fonction linéaire telle que :

Toute application linéaire est de la forme  ; il suffit pour la déterminer de trouver le coefficient a.

En remplaçant x par 12, on obtient : .

En identifiant les écritures et , on déduit que a × 12 = 44, donc , soit .

La fonction linéaire cherchée est donc : .

1.2. On a affaire à une situation de proportionnalité

Exemple 1 : une automobile roule à la vitesse constante de 110 km/h. On veut démontrer que la distance parcourue (en km) par cette automobile est une fonction linéaire de la durée (en h) du parcours et déterminer cette fonction linéaire.

Rappelons la formule d = v × t, où d désigne la distance parcourue, v la vitesse et t la durée du parcours. Ici, v = 110 km/h, donc d = 110t (d en kilomètres et t en heures) ; par conséquent, la fonction qui à la durée du parcours fait correspondre la distance parcourue est : . Il s'agit bien d'une fonction linéaire, et son coefficient est 110, c'est-à-dire la vitesse de l'automobile.

Exemple 2 : un commerçant décide de faire une remise de 30 % sur tous les articles de son magasin. On veut démontrer que le prix après réduction est une fonction linéaire du prix initial et déterminer cette fonction linéaire.

Appelons x le prix initial d'un article. Le prix après réduction sera alors égal à : , soit

.

Par conséquent, la fonction qui au prix initial fait correspondre le prix après réduction est : . Il s'agit bien d'une fonction linéaire, et son coefficient est 0,7.

Exemple 3 : on verse de l'eau dans un verre qui a la forme d'un cylindre de révolution de 12 cm de hauteur et de 8 cm de diamètre. On veut démontrer que la fonction qui à la hauteur h (en cm) de l'eau dans le verre fait correspondre le volume (en cm3) d'eau est une fonction linéaire et déterminer cette fonction linéaire.

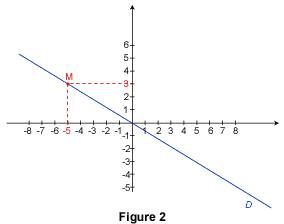
Rappelons que le volume V d'un cylindre de révolution de rayon r et de hauteur h est donné par la formule :

V =  r2h.

Le diamètre du cylindre est égal à 8 cm, son rayon est donc égal à 4 cm.

Le volume d'eau correspondant à une hauteur de h cm dans le verre est donc : V =   × 42 × h = 16 h.

Par conséquent, la fonction qui à la hauteur d'eau dans le verre fait correspondre le volume d'eau est :  ; il s'agit bien d'une fonction linéaire, et son coefficient est 16 .

2. Déterminer une fonction linéaire par un graphique

Exemple : on veut déterminer la fonction linéaire représentée sur la figure par la droite D.

On détermine par lecture graphique les coordonnées d'un point M (distinct de O) de la droite : ici M a pour coordonnées (–5 ; 3).

Notons la fonction linéaire à déterminer. Dire que le point M est sur la droite qui représente cette fonction linéaire, c'est dire que . D'autre part, en remplaçant x par –5 dans l'écriture , on obtient .

En identifiant ces deux écritures, on obtient : a × (–5) = 3, soit a = 3 ÷ (–5) = –0,6.

La fonction linéaire cherchée est donc : .

Remarque : cette méthode se ramène à celle qui est utilisée dans l'exemple du paragraphe 1.1 puisque la lecture du graphique permet de déterminer les coordonnées d'un point de la droite (distinct de O), ce qui fournit un nombre non nul et son image par la fonction linéaire.