Déterminer une aire par le découpage

On sait que l'aire A d'un rectangle dont les dimensions sont l et L est donnée par la formule A = l× L (A, L et l devant être exprimés dans des unités correspondantes).

Cette formule suffit pour calculer l'aire de certaines surfaces polygonales : selon quels procédés ?

1. Aire de triangles

1.1. Triangles rectangles
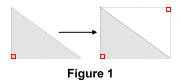
Pour déterminer l'aire d'un triangle rectangle, on complète le triangle de façon à obtenir un rectangle.

On observe, sur la figure, que l'aire du triangle rectangle est égale à la moitié de l'aire du rectangle.

1.2. Triangles non rectangles
Si un triangle n'a pas d'angle droit, on trace une hauteur ; on obtient alors deux triangles rectangles. En appliquant la méthode précédente, on calcule l'aire de chacun des triangles rectangles et on en déduit l'aire du triangle initial.

2. Aires de quadrilatères particuliers

2.1. Parallélogrammes
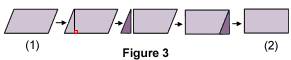
Sur la figure 3, on voit qu'un parallélogramme (1), dont on connaît un côté et la hauteur correspondante, a la même aire qu'un rectangle (2) de même base et de même hauteur.

2.2. Losanges
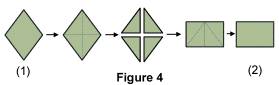
Sur la figure 4, on voit qu'un losange (1), dont on connaît les deux diagonales, a une aire égale à celle d'un rectangle (2) dont la longueur est égale à la petite diagonale du losange et la largeur est égale à la moitié de la grande diagonale du losange.

3. Autres cas
La surface présentée ci-dessous n'est pas une surface polygonale car son contour contient des lignes courbes.

Pour en calculer l'aire, il suffit de considérer qu'elle est formée d'un rectangle auquel on a retiré deux demi-disques ; à partir de ceux-ci, on reconstitue un disque.

L'aire d'un disque étant donnée par la formule A = 2 × 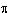  × R × R, la connaissance des dimensions du rectangle et du rayon du cercle suffit pour trouver l'aire de la surface initiale.