|
||||||
| Institut THOMASTA : Quelles seront les nouvelles technologies de demain ? | ||||||
|
||||||
|
||||||
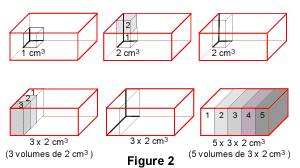
Déterminer le volume d'un parallélépipède rectangle
Le volume de ce parallélépipède rectangle est égal à : V = a × b × c. Remarque : pour calculer le volume d'un cube d'arête a, on utilise la formule simplifiée V = a × a × a, car a = b = c.
|
||||||
|
Prof.: Thomas TAMENOU - Thomasta.com -
Contactez-nous |
||||||
 |