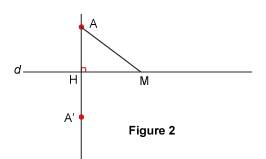
Déterminer la distance d'un point à une droite

On cherche à tracer un segment le plus court possible joignant un point à une droite.

Faut-il utiliser une équerre et, si oui, pourquoi ?

1. La distance d'un point à une droite

1.1. Propriété

Soit une droite d et A un point du plan. Soit H le pied de la perpendiculaire à d passant par A. H est le point de d le plus proche de A.

On voit sur la figure que, si M est un point de la droite distinct de H, alors AM > AH.

1.2. Démonstration

Notons d'abord que la propriété est vraie si A est sur d. En effet, dans ce cas de figure, H = A donc AH = 0 et si M est distinct de H (et donc de A), alors AM > 0.

Considérons ensuite le cas où A n'appartient pas à d. Reprenons la figure 1 et construisons le symétrique A' de A par rapport à d.

Par construction, la droite (AA') est perpendiculaire à d. Les points A, H et A' sont donc alignés et H est le milieu du segment [AA']. On a donc AA' = 2AH. (1)

De plus M est sa propre image par la symétrie axiale d'axe d et comme une symétrie axiale conserve les longueurs, A'M = AM. (2)

Considérons les trois points A, A' et M. L'inégalité triangulaire permet d'écrire : .

En utilisant les égalités (1) et (2), il vient : , d'où en simplifiant par 2 : .

Ce que l'on voulait démontrer.

1.3. Définition

Soit une droite d. Soit A un point et H le pied de la perpendiculaire à d passant par A.

La longueur AH s'appelle la distance du point A à la droite d.

On a vu (dans le paragraphe 1.1.) que c'est la plus petite distance entre A et un point de d.

2. Conséquences

2.1. L'hypoténuse du triangle rectangle

Propriété : soit un triangle ABC rectangle en A, l'hypoténuse [BC] est le côté le plus long.

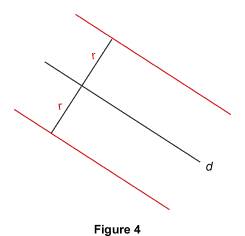
En effet :

la distance de B à la droite (AC) est BA donc BC > BA ;

de même : BC > AC.

Ce qui montre bien que l'hypoténuse est plus longue que chacun des deux autres côtés.

2.2. L'ensemble des points situés à une distance donnée d'une droite donnée

Propriété : soit une droite d et r un réel positif. L'ensemble des points qui se trouvent à la distance r de d est constitué de deux droites parallèles à d.

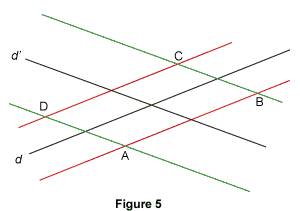
Application : soit d et d' deux droites sécantes. Trouver les points se trouvant à 2 cm de d et à 3 cm de d'.

On a tracé en rouge l'ensemble des points situés à 2 cm de d, et en vert l'ensemble des points situés à 3 cm de d'.

Ces quatre droites se coupent en A, B, C et D.

Ces quatre points se trouvent à 2 cm de d et à 3 cm de d'. Ils répondent donc au problème posé.