 |
||||||
| Institut THOMASTA : Quelles seront les nouvelles technologies de demain ? | ||||||
|
||||||
|
||||||
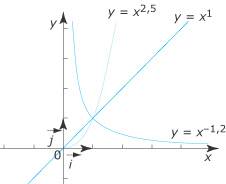
Croissances comparées Notre objectif est ici de comparer les fonctions logarithme népérien et exponentielle de base e aux fonctions puissances d’exposant réel. Les résultats obtenus, après factorisation de la puissance, permettent de lever des indéterminations du type « Parmi les multiples applications économiques des fonctions puissances, on retiendra le calcul d’un taux de variation sur un an, quand on connaît le taux d’évolution sur n années. 1. Quelles sont les caractéristiques des fonctions puissances d’exposant réel xα, définies sur ]0 ; +∞[ ? On sait que : y = xα équivaut à ln y = ln xα, ou encore à ln y = αln x. D’où : Donc Quelle est la dérivée de La fonction f, définie sur ]0 ; + En appliquant la formule D’où : Quel est le sens de variation de Étudions le signe de la dérivée Si Si On vérifie graphiquement le sens de variation en traçant les courbes d’équations
2. Quelles sont les limites de xα en 0 et en +∞ ? L’écriture Si
La limite en 0 est 0.
La limite en Si
L’axe des ordonnées est donc asymptote au voisinage de 0+.
L’axe des abscisses est donc asymptote au voisinage de 3. Comment croît la fonction exponentielle de base e par rapport aux fonctions puissances ? On étudie la limite en Exprimons d’abord le logarithme népérien de ce quotient : En factorisant x pour faire apparaître le quotient Au voisinage de Comme au voisinage de l’infini la fonction logarithme népérien a une limite infinie, alors La fonction exponentielle de base e tend donc vers l’infini infiniment plus vite que n’importe quelle fonction puissance. 4. Comment croît la fonction puissance par rapport à la fonction logarithme népérien ?
Or, comme Donc, quel que soit l’exposant réel 5. Comment détermine-t-on un taux équivalent ? Quelle est la solution de l’équation x Si Pour
Ainsi, si la population d’une ville passe en quatre ans de 30 000 à 18 000 habitants, le taux t de variation annuelle vérifie :
Isolons t en appliquant la règle précédente :
On observe donc une baisse de 12 % par an. À retenir Pour La dérivée de f(x) = xα est de la forme f’(x) = α xα – 1. Son signe est celui de Les limites de la fonction x exposant On constate que :
Pour a > 0 et l’égalité
|
||||||
|
Prof.: Thomas TAMENOU - Thomasta.com -
Contactez-nous |
||||||
 |
 d’où :
d’où : 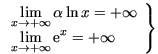 d’où :
d’où : 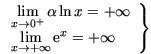 d’où :
d’où : 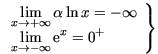 d’où :
d’où : 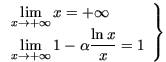 donc le produit implique :
donc le produit implique :