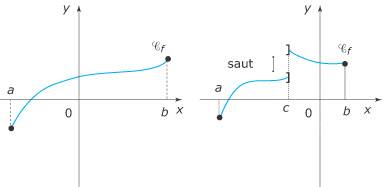
Continuité et théorème des valeurs intermédiaires

La notion de continuité permet d'énoncer correctement le théorème des valeurs intermédiaires. Ce dernier sert à déterminer le nombre de solutions d'une équation du type f(x) = k, où et où f est une fonction continue, et à en donner une valeur approchée ou un encadrement ; ceci est surtout intéressant lorsque l'on ne sait pas résoudre algébriquement une telle équation.

1. Qu'est-ce qu'une fonction continue en un point ? Sur un intervalle ?

Une fonction f, définie sur un intervalle ouvert contenant un réel a, est continue en a si

Une fonction f, définie sur un intervalle I ouvert, est continue sur I lorsque f est continue en tout réel a appartenant à I.

Une fonction f, définie sur un intervalle [a ; b], est « continue sur [a ; b] » lorsque :

En conséquence, lorsqu'une fonction est continue sur un intervalle de son ensemble de définition, on peut tracer sa représentation graphique « sans lever le crayon ».

Dans le cas contraire, la courbe présente un ou plusieurs « sauts ».

2. Quel est le lien entre continuité et dérivabilité ?

Toute fonction dérivable sur un intervalle I ouvert est continue sur I (et donc définie sur I).
Attention, la réciproque est fausse : ainsi, la fonction valeur absolue est continue sur mais pas dérivable en 0.

3. Quelles sont les fonctions continues sur tout intervalle de leur ensemble de définition ?

D'après le point précédent, toutes les fonctions dérivables sur chaque intervalle de leur ensemble de définition y sont continues ;  en particulier :

• les fonctions polynômes sont continues sur  ;

• les fonctions rationnelles sont continues sur tout intervalle de leur ensemble de définition ;

• la fonction racine carrée est continue sur  ;

• les fonctions cosinus et sinus sont continues sur  ;

• la fonction tangente est continue sur tout intervalle de son ensemble de définition.

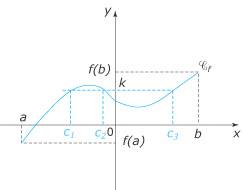
4. Qu'est-ce que le théorème des valeurs intermédiaires ? À quoi sert-il ?

Le théorème des valeurs intermédiaires s'énonce ainsi :

soit f une fonction définie et continue sur un intervalle I, et a et b deux réels de I ; pour tout réel k compris entre f(a) et f(b), il existe (au moins) un réel c compris entre a et b tel que f(c) = k.

Ce théorème a pour corollaire : si f est une fonction continue et strictement monotone sur un intervalle I alors, pour tout réel k de l'intervalle J = f(I), l'équation f(x) = k admet une unique solution dans I.

Remarques :

• On convient que, dans les tableaux de variation, les flèches obliques traduisent la continuité et la stricte monotonie de la fonction sur l'intervalle considéré.

• Le théorème des valeurs intermédiaires sert notamment à déterminer le nombre de solutions d'une équation et à donner un encadrement ou une valeur approchée de ces solutions.

À retenir

Une fonction f, définie sur un intervalle ouvert contenant un réel a, est continue en a si

Si une fonction f est dérivable sur un intervalle, alors elle est continue sur cet intervalle. Attention, la réciproque est fausse : une fonction continue n'est pas nécessairement dérivable.

Si f est une fonction continue et strictement monotone sur un intervalle I, alors, pour tout réel k de l'intervalle J = f(I), l'équation f(x) = k admet une unique solution dans I.

Ce corollaire du théorème des valeurs intermédiaires est très utile pour déterminer le nombre de solutions d'une équation du type f(x) = k et donner une valeur approchée ou un encadrement de ces solutions.