Construire les médianes d'un triangle et déterminer son centre de gravité

Dans un triangle, on peut tracer trois médianes.

Quelles propriétés possèdent les droites ainsi obtenues et qu'appelle-t-on centre de gravité du triangle ?

1. Les médianes d'un triangle

Une médiane d'un triangle est une droite qui passe par un sommet du triangle et le milieu du côté opposé à ce sommet.

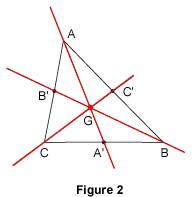
Remarques :

le mot médiane désigne aussi le segment joignant un sommet et le milieu du côté opposé à ce sommet (le segment [AA'] sur la figure 1) ;

dans un triangle, il y a trois médianes (autant que de sommets) ;

une médiane partage un triangle en deux triangles de même aire.

2. Le centre de gravité d'un triangle

2.1. Propriétés

Dans un triangle, les trois médianes sont concourantes. Leur point de concours est appelé centre de gravité du triangle.

Remarque : en pratique, il suffit de tracer deux médianes pour trouver le centre de gravité.
2.2. Position du centre de gravité

Le centre de gravité d'un triangle se trouve aux de chaque médiane, à partir du sommet.

Sur la figure 2 : , et .

Le centre de gravité d'un triangle se trouve donc toujours à l'intérieur du triangle.