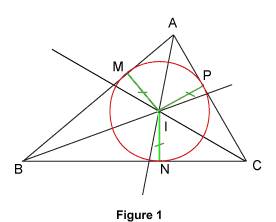
Construire les bissectrices d'un triangle et tracer le cercle inscrit dans le triangle

Si on dessine un cercle, il est facile de tracer trois tangentes à ce cercle qui en général font apparaître un triangle.

Mais, si on part d'un triangle, peut-on construire un cercle tangent aux trois côtés de ce triangle ?

1. Les bissectrices d'un triangle

Définition : la bissectrice d'un angle est la droite qui partage cet angle en deux angles de même ouverture.

Propriétés :

la bissectrice de l'angle est l'axe de la symétrie qui échange les deux demi-droites [Ox) et [Oy) ;

les points de la bissectrice de l'angle sont équidistants des supports des demi-droites [Ox) et [Oy).

La deuxième propriété permet de justifier la construction, à la règle et au compas, de la bissectrice d'un angle b.

L'expression bissectrices d'un triangle désigne les bissectrices des angles de ce triangle. Un triangle a donc trois bissectrices.

2. Le cercle inscrit dans un triangle

2.1. Propriété

Les trois bissectrices d'un triangle sont concourantes. Leur point de concours est à la même distance des trois côtés du triangle ; il est donc le centre du cercle tangent aux trois côtés du triangle.

Remarque : ce cercle est appelé cercle inscrit dans le triangle. Le mot inscrit vient du latin et signifie « écrit dedans ».

2.2. Construction du cercle inscrit dans un triangle

Il faut d'abord trouver le centre I ; c'est le point de concours des bissectrices du triangle. En pratique, il suffit de construire deux bissectrices pour trouver le centre du cercle inscrit.

Il faut ensuite trouver le rayon. Pour cela on trace une droite perpendiculaire à un côté et passant par I ; elle coupe le côté en M.

On trace alors le cercle de centre I et passant par M ; c'est le cercle inscrit dans le triangle.

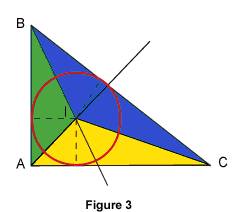
2.3. Calculer le rayon du cercle inscrit dans un triangle particulier

Dans la figure 3, AB mesure 3 cm, AC mesure 4 cm et BC, 5 cm.

À l'aide de la réciproque de la propriété de Pythagore, on peut démontrer que ABC est rectangle en A.

La mesure en cm² de son aire est égale à , soit 6.

Calculons cette mesure, d'une deuxième façon, en additionnant les aires des trois triangles coloriés.

Dans le triangle ABI, la hauteur relative à la base AB est égale au rayon r du cercle inscrit.

L'aire du triangle ABI est égale à , celle de ACI est égale à et celle de BCI à .

En les additionnant, on obtient , soit 6r = 6 ce qui donne r = 1 cm.

Généralisation : considérons un triangle ; si on note S son aire, P son périmètre et r le rayon de

son cercle inscrit, on a .