Comportements asymptotiques

Lorsqu’une fonction est définie sur un intervalle fermé, on peut calculer facilement l’image de tous les réels de cet intervalle, y compris celle des extrémités, et ainsi représenter graphiquement la fonction. Cependant, l’ensemble de définition d’une fonction peut contenir des intervalles ouverts : ouverts sur l’infini ou ouverts sur une valeur interdite par l’écriture de la fonction, par exemple une valeur qui annule un dénominateur. Quel est alors le comportement de la fonction au voisinage de ces valeurs extrêmes ?

Quand la courbe représentative d’une fonction prend l’allure d’une droite au voisinage de la valeur interdite ou de l’infini, on dit que cette droite est une asymptote à la courbe. Cette asymptote peut être verticale dans le cas d’une valeur interdite, ou bien horizontale ou oblique à l’approche de l’infini. Comment détermine-t-on l’équation de ces asymptotes ?

1. Quels sont les comportements de la fonction inverse « 1 sur x » en zéro et plus l’infini ?

La fonction inverse se représente, sur , par une branche d’hyperbole.

La fonction inverse est décroissante sur . Lorsque x s’approche de 0, s’approche de l’infini.

On écrit : ( signifie que x s’approche de 0 par valeurs supérieures à 0).

Graphiquement, la courbe s’approche de l’axe des ordonnées lorsque x s’approche de 0. L’axe des ordonnées est asymptote à la courbe au voisinage de 0.

De même, s’approche de 0, lorsque x tend vers l’infini.

On écrit : ( s’approche de 0 par valeurs supérieures à 0).

Graphiquement, la courbe s’approche de l’axe des abscisses lorsque x devient très grand. L’axe des abscisses est asymptote à la courbe au voisinage de  .

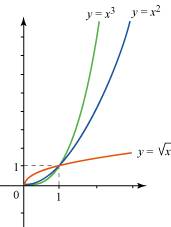
2. Quel est le comportement en plus l’infini des fonctions racine, carré et inverse ?

Pour x > 1, l’image par la fonction racine est inférieure à l’image par la fonction carré, elle-même inférieure à l’image par la fonction cube.

Or tend vers l’infini lorsque x tend vers l’infini. Donc : .

Ainsi, comme la limite de est infinie lorsque x tend vers l’infini, il en est forcément de même

pour x2 et x3. D’où : et .

3. Peut-on toujours déterminer la limite de la somme, du produit, du quotient ou de la composée de deux fonctions ?

Les limites des fonctions de référence (fonctions affines, racine, inverse, carré ou cube) aux bornes de leur ensemble de définition sont connues. Pour connaître la limite de leur somme, de leur produit ou de leur composée, il suffit de transposer ces opérations à leurs limites. Toutefois, dans quatre cas on a une forme indéterminée et on ne peut pas conclure sans transformer l’écriture.

1er cas : «   ». La limite de la fonction somme est indéterminée lorsque l’une des fonctions a pour limite et l’autre .

2e cas : «   ». Il y a indétermination lorsque la fonction est le produit de deux fonctions dont l’une a pour limite 0 et l’autre l’infini.

3e cas : «   » et 4e cas : «   ». La limite de la fonction quotient est indéterminée lorsque les deux fonctions ont pour limite 0 ou pour limite l’infini.

La limite à l’infini d’une fonction polynôme est la limite de son terme de plus haut degré.

On a par exemple : .

La limite à l’infini d’une fonction rationnelle est la limite du quotient de ses termes de plus haut degré. On a par exemple : .

4. Comment sait-on qu’une courbe admet une asymptote verticale ou horizontale ?

La droite d’équation x = a est asymptote verticale à la courbe d’équation , définie sur , lorsque la fonction admet en a une limite infinie : .

La droite d’équation y = b est asymptote horizontale à la courbe d’équation au voisinage de (respectivement ), lorsque la fonction tend vers la limite finie b quand x

tend vers (respectivement ) : (respectivement ).

5. Comment sait-on qu’une courbe admet une asymptote oblique ?

La droite d’équation y = ax + b est asymptote oblique à la courbe d’équation au

voisinage de (respectivement ) lorsque : (respectivement

).

Si , l’écart entre l’image donnée par la fonction et l’image donnée par la fonction affine représentée par l’asymptote, s’approche de 0 par valeurs positives ; la courbe est alors au-dessus de l’asymptote.

De même, si , cet écart s’approche de 0 par valeurs négatives et la courbe est au-dessous de l’asymptote.

À retenir absolument

La fonction inverse , définie sur , a une limite nulle en et une limite infinie

en 0 : et . Les axes des abscisses et des ordonnées sont les asymptotes à sa représentation graphique.

Une fonction polynôme est définie sur . Sa limite à l’infini est celle de son terme de plus haut degré.

Une fonction rationnelle est le quotient de deux fonctions polynômes ; sa limite à l’infini est donc la limite du quotient de ses termes de plus haut degré.

Au voisinage des valeurs interdites qui annulent le dénominateur, on calcule séparément la limite du numérateur et du dénominateur.

Quatre formes indéterminées nécessitent une transformation pour pouvoir conclure :

«   », «   », «   » et «   ».

Une courbe admet une asymptote verticale lorsqu’en un point la limite de la fonction est infinie. L’asymptote est horizontale lorsque la limite à l’infini de la fonction est un nombre réel.

Elle est oblique, de la forme y = ax + b, lorsque l’écart f(x) - (ax + b) est proche de 0 au voisinage de l’infini.