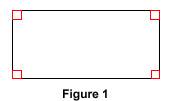
Caractériser et construire un rectangle, un carré

Les carrés et les rectangles sont des quadrilatères particuliers. Le carré a pour originalité d'être à la fois un rectangle et un losange.

Quelles sont les propriétés de ces figures et comment peut-on les tracer ?

1. Les rectangles

1.1. Définition

Un rectangle est un quadrilatère qui a quatre angles droits.

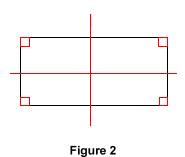
Grâce à la définition précédente, on peut démontrer également que :

les côtés opposés d'un rectangle sont parallèles deux à deux ;

les côtés opposés d'un rectangle ont deux à deux la même longueur ;

tout rectangle a deux axes de symétrie, qui sont les médiatrices de ses côtés. Réciproquement, si dans un quadrilatère les médiatrices des côtés sont des axes de symétrie, alors ce quadrilatère est un rectangle.

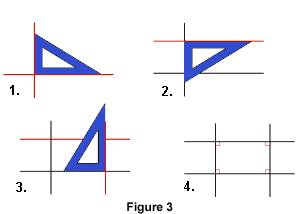
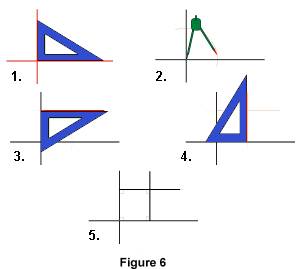
1.2. Construction

Les figures ci-dessous montrent les étapes de la construction d'un rectangle. Si les longueurs des côtés sont données, on utilise une équerre graduée.

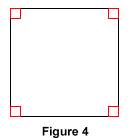
2. Les carrés

2.1. Définition

Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de la même longueur.

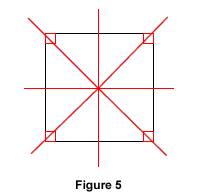
Grâce à la définition précédente, on peut démontrer également que tout carré a quatre axes de symétrie, qui sont les médiatrices des côtés opposés et les diagonales. Réciproquement, si dans un quadrilatère les médiatrices des côtés et les diagonales sont des axes de symétrie, alors ce quadrilatère est un carré.

Remarques :

d'après la définition d'un rectangle, on peut dire que, si un quadrilatère est un carré, alors ce quadrilatère est un rectangle ;

d'après la définition d'un losange, on peut dire que, si un quadrilatère est un carré, alors ce quadrilatère est un losange.

2.2. Construction

Il suffit de reprendre la construction du paragraphe 1.2. en prenant soin de marquer des points à égale distance du sommet de l'angle droit de départ.