Caractériser et construire un cerf-volant

Un cerf-volant est un quadrilatère particulier qui n'a qu'un axe de symétrie. Quelles sont les propriétés de cette figure et comment peut-on la tracer ?

1. Définition

Un cerf-volant est un quadrilatère dont une diagonale est médiatrice de l'autre. La médiatrice d'un segment est la droite qui est perpendiculaire à ce segment et qui passe par son milieu.

Figure 1 : la droite (BD) est la médiatrice du segment [AC].

Figure 2 : les segments [AE] et [BD] sont les diagonales de ABED : la diagonale [AE] se trouvant à l'extérieur de ABED. Là encore, la droite (BD) est la médiatrice du segment [AE].

ABED est un cerf-volant.

Grâce à la définition précédente, on peut également démontrer que :

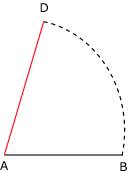
Réciproquement, si dans un quadrilatère, une diagonale est axe de symétrie, alors ce quadrilatère est un cerf-volant.

Par ailleurs, les angles opposés d'un cerf-volant ont la même mesure.

Remarque : un losange est un cerf-volant particulier.

2. Construction

On veut construire un cerf-volant avec la règle et le compas. La série de figures ci-dessous montre la construction d'un cerf-volant de côté 3 cm et 5 cm.

Figure 1 : avec la règle, on trace un segment de longueur 5 cm.

Figure 2 : avec le compas, on trace un arc de cercle de centre A passant par B.

Figure 3 : on place un point D où l'on veut sur l'arc tracé.

Figure 4 : avec la règle on trace le segment [AD].

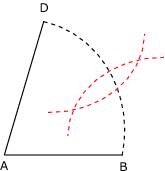
Figure 5 : avec le compas, on trace un arc de cercle de centre D et de rayon 3 cm, puis un arc de cercle de centre B et de rayon 3 cm.

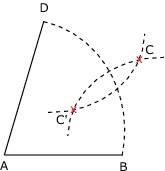
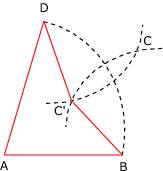
Figure 6 : les deux arcs de cercles se coupent en C et C'.

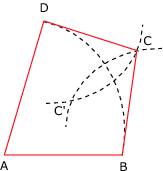
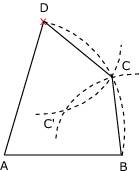
Figure 7 et 8 : on termine le dessin en traçant l'un des deux cerfs-volants obtenus.

ou

Remarque : on obtient d'autres cerfs-volants ayant les mêmes caractéristiques en donnant une autre position au point D. Par exemple :

ou