Calcul intégral

Calculer l'intégrale d'une fonction, c'est d'abord déterminer une primitive de cette fonction ou vérifier qu'une fonction donnée en est une primitive. Lorsque la fonction est positive, l'intégrale représente une aire sur la représentation graphique.

En économie, elle peut être assimilée au produit de deux grandeurs et permettre de définir le coût total ou le bénéfice total sur une période donnée. La valeur moyenne représente alors le coût moyen ou le bénéfice moyen sur cette période.

1. Comment calcule-t-on une intégrale ?

Si une fonction f est définie et dérivable sur un intervalle [a ; b], alors elle admet une primitive F telle que F' (x) = f(x).

L'intégrale de a à b, notée , est donnée par la différence F(b) – F(a).

On retiendra :

Par exemple :

2. Une intégrale peut-elle être négative ?

Oui, c'est le cas :

• lorsque l'on intègre une fonction négative et que la borne inférieure de l'intégrale est plus petite que la borne supérieure ; 

• lorsque l'on intègre une fonction positive et que la borne inférieure de l'intégrale est plus grande que la borne supérieure.

3. Quel est le lien entre une aire et une intégrale ?

Ce n'est que lorsque la fonction f est positive sur l'intervalle [a ; b] que l'intégrale est égale à l'aire de la partie du plan comprise entre l'axe des abscisses, les droites d'équations x = a, x = b et la courbe de f.

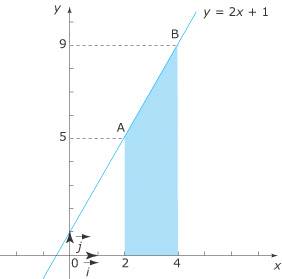
Ainsi, le trapèze délimité par les droites d'équations y = 2x + 1, x = 2, x = 4 et l'axe des

abscisses a pour aire :  ; soit 14 unités d'aire.

Si f est négative sur l'intervalle [a ; b], alors l'aire est égale à :

Si f change de signe sur l'intervalle [a ; b], on pensera à se ramener aux deux cas précédents en découpant l'intervalle.

4. Comment calcule-t-on la valeur moyenne d'une fonction sur un intervalle ?

La valeur moyenne d'une fonction f sur un intervalle [a ; b] est égale au réel

Cette notion est utile en sciences physiques et en sciences économiques lorsque la variable dont on veut calculer la valeur moyenne est continue et prend un nombre infini de valeurs.

5. Quelles sont les propriétés de l'intégrale ?

L'intégrale est linéaire : si et sont deux nombres réels,

L'intégrale de la somme de deux fonctions est donc la somme de leurs intégrales.

Attention, en général ce n'est pas vrai pour un produit ou un quotient.

L'intégrale vérifie la relation de Chasles :

Pour calculer une aire, on peut donc faire une partition de l'intervalle de définition, afin que la fonction ait le même signe sur chacun des intervalles de cette partition.

L'intégrale respecte le sens des inégalités :

si , alors

On peut ainsi encadrer à partir d'un encadrement de f(x) sur l'intervalle [a ; b].

6. Comment vérifier le calcul d'une intégrale à l'aide de la calculatrice ?

Les calculatrices les plus élaborées possèdent une touche à cet effet.

Pour calculer , il suffit alors d'afficher : intégrale (f(x), x, a, b).

Pour les autres calculatrices, on peut utiliser un programme calculant l'aire de 100 trapèzes compris entre la courbe et l'axe des abscisses :

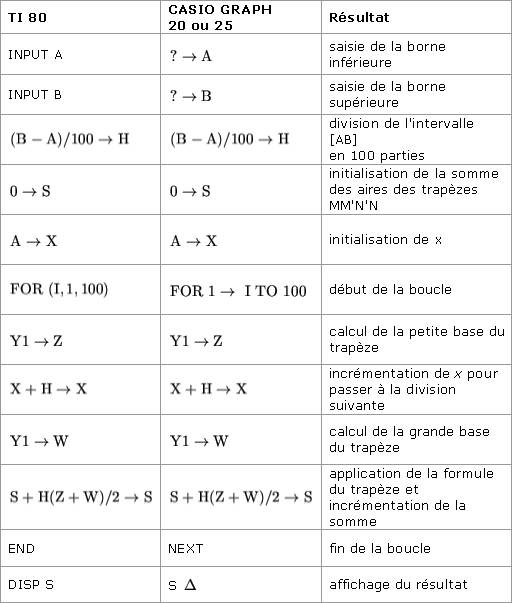
Programme :

Pour Y1, taper schift Yvars (sur la TI 80) ou Vars puis Graph (sur la CASIO GRAPH 20 ou 25).

Exécution :

Afficher les bornes A et B, puis la fonction Y1.

À retenir

L'intégrale de a à b de la fonction f, définie et dérivable sur un intervalle [a ; b] et de primitive F, est donnée par :

Lorsque la fonction f est positive sur l'intervalle [a ; b], l'intégrale est égale à l'aire de la partie du plan comprise entre l'axe des abscisses, les droites d'équations x = a et x = b et la courbe de f.

La valeur moyenne de f sur l'intervalle [a ; b] est égale au réel

L'intégrale de la somme de deux fonctions est la somme de leurs intégrales.