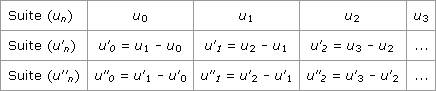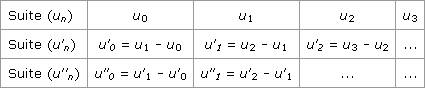Autres exemples de croissance

Considérons la suite arithmétique de terme général et la suite géométrique .

Ces deux suites sont croissantes. Dans le premier cas, la croissance est linéaire (sa représentation graphique est une droite), dans le second cas, elle est exponentielle.

Il existe cependant d'autres types de suites, par exemple , qui correspondent à d'autres modèles de croissance. De ces suites, on peut dire que ce sont des suites aux différences secondes constantes. Qu'est-ce que cela signifie ?

1. Qu'appelle-t-on suite des différences premières ? Suite des différences secondes ?

Soit une suite (un). On pose : . On dit que la suite (u'n) est la suite des différences premières de la suite (un).

On remarquera que, si la suite (un) est arithmétique, la suite des différences premières de (un) est constante.

On pose maintenant : . On dit que la suite (u''n) est la suite des différences secondes de la suite (un). Pour obtenir les termes de cette suite, on ajoute une ligne au tableau précédent.

2. Qu'est-ce qu'une suite aux différences secondes constantes ?

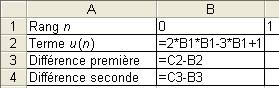
La suite (un) est dite une suite aux différences secondes constantes si la dernière ligne du tableau ci-dessus est composée de nombres égaux. C'est le cas si la suite des différences premières de (un) est une suite arithmétique, c'est-à-dire, s'il existe a et b, tels que : .

La forme générale des suites aux différences secondes constantes est (par exemple : ).

3. Comment calculer les différences secondes d'une suite à l'aide d'un tableur ?

Un tableur permet de calculer rapidement les différences secondes d'une suite. Voici le tableau obtenu à partir de la suite de terme général : .

Les cellules de ce tableau contiennent les formules suivantes :

Notons que le tableau n'est constitué que de références relatives.

4. Qu'est ce qu'une croissance quadratique ? Une croissance cubique ?

Une croissance quadratique est un phénomène de croissance que l'on peut modéliser par une suite de la forme : .

Par exemple, la suite des carrés définie par est une suite quadratique.

Une croissance cubique peut quant à elle être modélisée par une suite de la forme : .

Par exemple, la suite des cubes définie par est une suite cubique.

À retenir absolument

Une suite aux différences secondes constantes peut toujours s'exprimer sous la forme : .

Réciproquement, toutes les suites de la forme sont des suites aux différences secondes constantes.