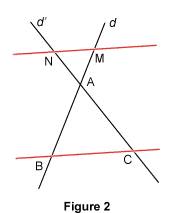
Appliquer le théorème de Thalès (3e)

Thalès était un mathématicien grec qui vécut aux viie et vie siècles avant notre ère. La légende prétend qu'il se rendit en Égypte et y mesura la hauteur de la pyramide de Khéops. Il aurait pour cela utilisé le théorème qui porte aujourd'hui son nom. En fait, cette propriété était déjà connue des Babyloniens bien avant Thalès et elle ne sera démontrée que plus tard.

1. Le théorème de Thalès

Soit d et d' deux droites sécantes en A. On suppose que B et M sont deux points de d distincts de A, et que C et N sont deux points de d' distincts de A.

Si les droites (BC) et (MN) sont parallèles, alors .

Ce théorème peut être appliqué dans deux cas de figure, appelés « situations de Thalès ».
Première situation : le point M est sur le segment [AB] et le point N est sur le segment [AC].

Il s'agit là de la propriété étudiée en quatrième.

Deuxième situation : le point A est sur le segment [MB] et le point A est sur le segment [NC].

Remarques :

chacune de ces deux situations fait apparaître deux triangles AMN et ABC dont les côtés sont deux à deux parallèles ;

on notera que dans les égalités , les côtés d'un triangle (ici AMN) figurent tous au numérateur, et les côtés parallèles correspondants de l'autre triangle (ici ABC) figurent tous au dénominateur ;

les égalités de ces trois rapports indiquent que l'un des triangles est un agrandissement de l'autre (sauf si ces rapports sont égaux à 1 dans la deuxième situation, auquel cas les deux triangles ont les mêmes dimensions).

2. Applications

2.1. Calculer des longueurs

Énoncé : sur la figure 3, les droites (AC) et (BD) sont parallèles. L'unité de longueur est le centimètre. On donne OA = 2,5 ; OB = 3 ; OC = 2 ; DB = 4,8. On veut calculer les longueurs OD et AC.

Résolution

Puisque les droites (AC) et (BD) sont parallèles, on peut appliquer le théorème de Thalès.

On obtient , donc .

À partir de , on obtient , soit OD = 2,4 cm.

À partir de , on obtient , soit AC = 4 cm.

2.2. Construire des points définis par des rapports de longueurs

Énoncé : soit A et B deux points distincts. On veut construire deux points I et J de la

droite (AB) tels que , sans utiliser les graduations de la règle.

Résolution :

On trace deux droites parallèles d et d' coupant respectivement la droite (AB) en A et B. On choisit un écartement de compas que l'on prend comme unité de longueur dans tout ce qui va suivre ;

On place sur d un point E tel que EA = 4, puis on place le point F de d' situé du même côté de la droite (AB) que E tel que FB = 7. La droite (EF) coupe la droite (AB) en un point I.

Démontrons que ce point I vérifie l'égalité demandée : . Les droites (EA) et (FB) étant

parallèles par construction, on peut appliquer le théorème de Thalès. On obtient . En

remplaçant EA par 4 et FB par 7 dans l'égalité , on obtient l'égalité souhaitée : .

On place ensuite le point G distinct de E de la droite d tel que AG = 4 ; la droite (FG) coupe la droite (AB) en un point J.

Démontrons que ce point J vérifie l'autre égalité demandée : . Les droites (GA) et (FB)

étant parallèles par construction, on peut appliquer le théorème de Thalès. On obtient

. En remplaçant AG par 4 et BF par 7 dans l'égalité , on obtient l'égalité

souhaitée : .