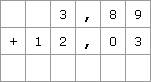
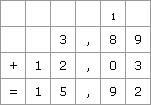
Additionner, soustraire des nombres décimaux

Lorsque l'on additionne ou soustrait des nombres décimaux, on obtient bien sûr un nombre décimal. Quelle technique appliquer quand on ne dispose pas de calculatrice ?

1. Cas où les écritures sont décimales

1.1. Les écritures ont le même nombre de décimales

Il suffit de placer dans une même colonne les chiffres de même nature.
Pour calculer par exemple 3,89 + 12,03, il suffit de disposer les calculs ainsi :

On aligne correctement les chiffres des parties entières ; puis, à droite de la virgule, on place les chiffres des dixièmes les uns sous les autres, de même pour les chiffres des centièmes, et ainsi de suite pour les autres décimales.

Il suffit alors d'effectuer l'addition selon la technique usuelle.

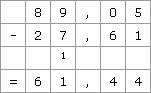
Pour la soustraction, on utilise la même méthode.

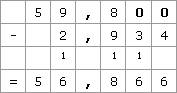
1.2. Les écritures n'ont pas le même nombre de décimales

En ajoutant des zéros à droite de la partie décimale, il est toujours possible de faire en sorte que des nombres décimaux soient écrits avec le même nombre de décimales.

Ainsi, 59,8 - 2,934 = 59,800 - 2,934. En disposant les chiffres de la même manière que dans le paragraphe 1.1, on trouve le résultat suivant :

2. Cas où les écritures sont fractionnaires

Il est toujours possible de se ramener au cas des écritures décimales en convertissant les écritures fractionnaires en écritures décimales.

Par exemple, pour effectuer la somme , il suffit de l'écrire : 31,007 + 6,109.

On trouve alors, en utilisant la méthode du paragraphe précédent, le résultat 37,116 que l'on peut réécrire ainsi :

.

Remarque : il est parfois plus rapide de ne pas convertir les écritures fractionnaires en écritures décimales.

Par exemple : .