|
|||||||||||||||||||||||||||||||||||||||
| Institut THOMASTA : Quelles seront les nouvelles technologies de demain ? | |||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||
LES INDICATEURS DE VALEUR CENTRALE, DE DISPERSION ET DE CONCENTRATION
Pour synthétiser une série de nombres, on utilise une valeur essentielle, la moyenne arithmétique. X = 5000 + 6000 + 7000 + 8000 + 10 000 = 7 200 F Les moyennes peuvent être tirées vers le haut ou vers le bas par le poids important de quelques éléments ; ainsi, dans un pays d’un million d’habitants où tout le monde gagnerait 4 000 francs sauf une personne qui gagnerait 4 milliards de francs, le revenu moyen serait de 8 000 francs. C’est pour cette raison qu’on préfère parfois le revenu médian au revenu moyen.
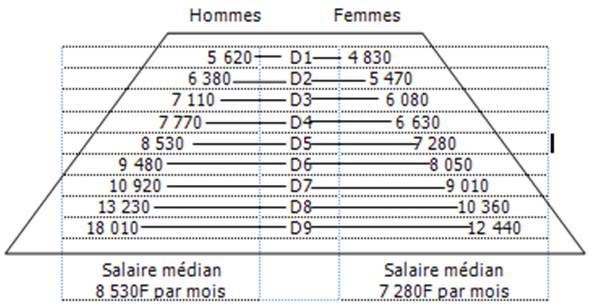
Une fois que les grandeurs d’une série ont été ordonnées selon un ordre croissant, la médiane permet de connaître la valeur qui partage le nombre d’observations en deux parts égales. Sur l’exemple utilisé lors de la présentation de la moyenne, la médiane est de 7 000F puisque deux valeurs (5 000F et 6 000F) sont inférieures à 7 000F et deux valeurs (8 000F et 10 000F) sont supérieures à 7 000F. Lorsque le nombre d’observations est pair, la médiane peut se situer entre deux observations. Exemple : six personnes gagnent respectivement 5000F, 5500F, 6500F, 7000F, 8000F et 10000F par mois, le revenu médian est situé entre 6500F et 7000F. On fait alors la moyenne arithmétique de ces deux valeurs ; on obtient un revenu médian de 6 750F. La médiane est une valeur centrale très significative. Il est par exemple important de savoir qu’en 1992 la moitié des hommes ont reçu un salaire net inférieur à 8 530F par mois alors que la moitié des femmes ont reçu un salaire net inférieur à 7 280F par mois.
Si les indicateurs de valeur centrale sont nécessaires pour caractériser une série, ils ne sont pas suffisants. Deux séries qui ont les mêmes valeurs centrales peuvent être très différentes de part et d’autre de cette valeur centrale. B = 8, 9, 10, 11, 12 Ces deux séries ont la même moyenne et la même médiane (10), mais les notes ne sont pas reparties de la même manière. Il est donc nécessaire d’étudier leur dispersion.
On cherche la moyenne des écarts à la moyenne mais comme il y a des valeurs au dessus de la moyenne et des valeurs au-dessous de la moyenne, la moyenne des écarts à la moyenne est égale à 0. Pour lever cette difficulté, on élève au carré les écarts à la moyenne et on calcule la racine carrée de la moyenne du carré des écarts à la moyenne. Exemple
N= 5 x = i = 1 = 36 000 = 7 200 n Tout se passé comme si les revenues se situaient, en moyenne à 1 720,50F en plus ou en moins du revenue moyen.
De la même façon que la médiane divise la série en deux groupes égaux, les 9 déciles divisent la série en 10 groupes égaux (chaque groupe contient 10% des observations). Le coefficient de dispersion est égal au rapport décile 9/Décile 1. Exemple Pour les hommes, le coefficient de dispersion D9/D1 est égale à 18 010/5 620 = 3,2. Cela signifie que le salaire au-dessus duquel se situent les 10% des salariés masculins les mieux rémunérés en 1992 est égal à 3,2 fois le salaire en dessous duquel se situent les 10% des salariés masculins les moins bien rémunérés. Pour les femmes, le coefficient de dispersion D9/D1 est égal à 12 440/4 830 = 2,6. Cela signifie que le salaire au-dessus duquel se situent les 10% des salariés féminins les mieux rémunérés en 1992 est égal à 2,6 fois le salaire en dessous duquel se situent les 10% des salariés féminins les moins bien rémunérés. Les hommes ont un salaire médian supérieur (de17,2%) au salaire médian des femmes. La dispersion des salaires des hommes est en outre plus forte que la dispersion des salaires des femmes (3,2 est > à 2,6).
On partage la population étudiée en 10 groupes égaux ; ils représentent chacun 10% de la population.
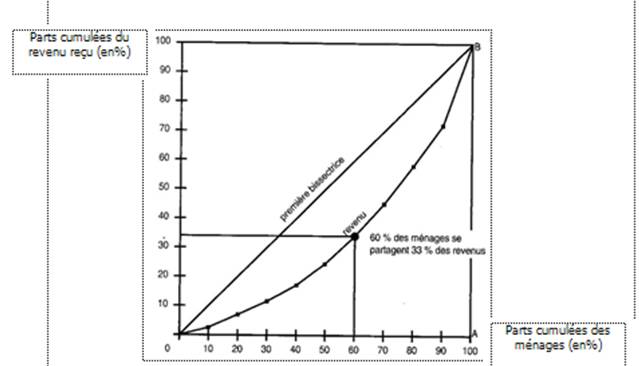
La concentration du revenu en 1986 Les 10% des ménages dont les revenus sont les plus faibles se partagent 2,2% des revenus. A partir de ces données, on trace la courbe de Lorenz.
La répartition aurait été parfaitement égalitaire si la courbe de Lorenz de la grandeur étudié avait été confondue avec la première bissectrice. 10% des ménages dont les revenus sont les plus faibles se partageraient 10% des revenus, 20% des ménages dont les revenus sont les plus faibles se partageraient 20% des revenus x% des ménages dont les revenus sont les plus faibles se partageraient x% des revenus, quel que soit le point de la diagonale. En revanche, on obtiendrait une répartition parfaitement inégalitaire si un seul salarié percevrait la totalité du revenu, les autres ne recevant rien. Sur le graphique, cette situation correspond à la courbe OAB formée par deux cotés du carré. En réalité, on se trouve quelque part entre ces deux situations extrêmes, quelque part entre la première bissectrice OB et la courbe OAB. Plus la courbe de Lorenz est proche de la première bissectrice, plus la concentration de la grandeur étudiée est faible. La concentration est donc d’autant plus forte que la courbe de la grandeur étudiée est loin de la première bissectrice. Ce coefficient égal à 0 indique une répartition parfaitement égalitaire.
|
|||||||||||||||||||||||||||||||||||||||
|
Prof.: Tchamgoue Buttinol Pierre - Thomasta.com -
Contactez-nous |
|||||||||||||||||||||||||||||||||||||||
 |