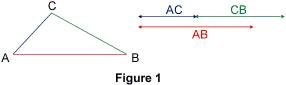
Utiliser l'inégalité triangulaire

Si l'on choisit trois longueurs au hasard, est-il possible de construire un triangle ayant pour dimensions les longueurs choisies ? Comment vérifier que la construction est possible ?

1. Les inégalités triangulaires

1.1. Avec trois points non alignés

Soit ABC un triangle. La longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.

Autrement dit, on a : AB < AC + CB ; BC < BA + AC et AC < AB + BC.

Remarque : ces inégalités s'appellent des inégalités triangulaires.

1.2. Avec trois points alignés

Soit A, B et C trois points, A et B étant distincts.

Si C appartient au segment [AB] , alors on a : AB = AC + CB ; BC < BA + AC et AC < AB + BC.

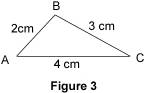
Réciproquement, soit A, B et C trois points, A et B étant distincts. Si AB = AC + CB, alors le point C appartient au segment [AB].

1.3. Avec trois points quelconques

De façon générale, quels que soient trois points A, B et C, on a :  ; et .

Remarque : ces inégalités sont prises au sens large, ce qui rend compte de toutes les dispositions des points (alignés ou non).

2. Exemples d'application

2.1. Exemple 1

Soit AB = 2 cm, BC = 3 cm et AC = 4 cm.

Les trois inégalités suivantes sont vérifiées : AB < AC + CB ; BC < BA + AC et AC < AB + BC. On peut donc construire un triangle ABC.

Remarque : AC étant la plus grande longueur, il suffit de vérifier que : AC < AB + BC.

2.2. Exemple 2

Soit AB = 3 cm, BC = 5 cm et AC = 2 cm.

BC = BA + AC donc le point A appartient au segment [BC].

2.3. Exemple 3

Soit AB = 7 cm, BC = 3 cm et AC = 2 cm.

L'inégalité AB < BC + AC n'est pas vérifiée ; donc, il n'existe pas de points A, B et C tels que : AB = 7 cm, BC = 3 cm et AC = 2 cm.