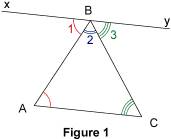
Utiliser la somme des angles d'un triangle

La somme des trois angles d'un triangle est égale à 180°.

Comment peut-on utiliser cette propriété pour calculer les angles d'un triangle ?

1. Démontrer la propriété

Sur la figure 1, ABC est un triangle quelconque. La droite (xy) est la parallèle à (AC) passant par B.

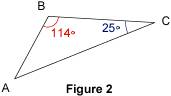
Les angles et  sont alternes internes ; ils ont donc la même mesure puisque les droites (xy) et (AC) sont parallèles. Donc .

De même, les angles et ont la même mesure. Donc .

On sait que puisque est un angle plat.

On en déduit que, dans le triangle ABC, .

2. Calculer des angles

2.1. Dans un triangle quelconque

Exemple : on veut calculer l'angle Â du triangle ABC.

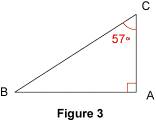
On applique la règle :  + 114° + 25° = 180°.

D'où les calculs :  + 139° = 180° et  = 180° - 139° = 41°.

2.2. Dans un triangle rectangle

La somme des deux angles aigus d'un triangle rectangle est égale à 90°.

En effet, considérons un triangle ABC rectangle en A.

Alors :  = 90° donc , ce qui entraîne .

Exemple : on veut calculer l'angle  du triangle ABC rectangle en A représenté sur la figure 3.

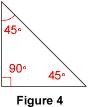
On applique la règle énoncée précédemment :  ; d'où : et .
L'angle  mesure 33°.

Remarque : les angles aigus d'un triangle rectangle et isocèle mesurent chacun 45°. En effet, ils ont la même mesure puisque le triangle est isocèle et leur somme doit être égale à 90° puisque le triangle est rectangle. Chacun mesure donc  degrés, c'est-à-dire 45°.

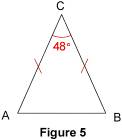
2.3. Dans un triangle isocèle

Exemple : on veut calculer les angles  et du triangle ABC isocèle en C.

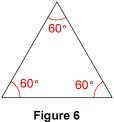
On applique la règle : . Comme ABC est isocèle en C, on a : ,

d'où :  + Â + 48° = 180° ; 2 + 48° = 180° ; 2 = 180°– 48° = 132° et .

L'angle Â (ainsi que l'angle  ) mesure 66°.

2.4. Dans un triangle équilatéral

Les trois angles d'un triangle équilatéral mesurent 60° chacun.

En effet, ils ont la même mesure puisque le triangle est équilatéral et leur somme est égale

à 180°. Ils mesurent donc chacun  degrés, c'est-à-dire 60°.