Reconnaître une situation de proportionnalité

Considérons les expressions suivantes :

• au supermarché, le prix d'un poulet est proportionnel à sa masse ;

• à vitesse constante, la consommation d'essence d'une voiture est proportionnelle à la distance parcourue.

Chacune d'elles évoque une situation de proportionnalité.

Qu'est-ce que cela signifie ? À quelles conditions peut-on dire d'une situation qu'il s'agit d'une situation de proportionnalité ?

1. Reconnaître un tableau de proportionnalité

Exemple :

Le tableau ci-dessus est un tableau de proportionnalité ; en effet, les nombres de la seconde ligne sont respectivement égaux à 5 fois ceux de la première ligne :

2 × 5 = 10
7 × 5 = 35
0,8 × 5 = 4

Définition : un tableau de proportionnalité est un tableau (formé de deux lignes de nombres) pour lequel il existe un nombre k tel que les nombres de la seconde ligne sont respectivement égaux à k fois ceux de la première ligne.

Le nombre k s'appelle le coefficient de proportionnalité.

2. Applications

2.1. Exemple 1 : le prix d'un poulet

On a relevé les masses et les prix de quatre poulets dans un supermarché et on a consigné les résultats dans le tableau ci-dessous.

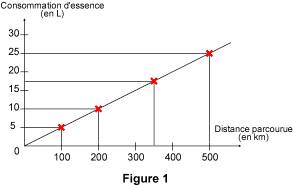
Effectuons les calculs suivants :

6,25 ÷1,250 = 5 donc 1,250 × 5 = 6,25
1,700 × 5 = 8,5
2,300 × 5 = 11,5
2,520 × 5 = 12,6

Ces calculs montrent que le tableau ci-dessus est un tableau de proportionnalité. C'est en ce sens qu'il faut comprendre la phrase : « le prix d'un poulet est proportionnel à sa masse ».

Remarque : le coefficient de proportionnalité est égal à 5 ; 5 € serait le prix d'un poulet de 1 kg. Ce coefficient apparaît sur les étiquettes des poulets sous la forme suivante : « prix au kilogramme : 5 €/kg ».

2.2. Exemple 2 : la consommation d'une voiture

Le graphique présenté sur la figure donne la consommation d'essence d'une voiture en fonction de la distance parcourue à vitesse constante. On peut, par exemple, y lire que la voiture consomme 5 litres d'essence pour 100 kilomètres parcourus.

Tous les points du graphique sont alignés avec l'origine du repère. Cet alignement est caractéristique d'une situation de proportionnalité.

On peut mettre en évidence cette situation de proportionnalité en établissant un tableau (1re ligne : distance parcourue en km ; 2e ligne : consommation en L) à partir de valeurs du graphique ; on obtient le tableau de proportionnalité suivant :

Remarque : le coefficient de proportionnalité est égal à 0,05 (5 ÷ 100) ; c'est la consommation d'essence en L pour 1 km parcouru.

2.3. Exemple 3 : la dépense annuelle dans un club vidéo

Dans un club vidéo, on paye 18 € d'abonnement pour un an, puis 2 € par film loué.

La dépense annuelle est-elle proportionnelle au nombre de films loués ?

Considérons le tableau ci-dessous :

On dépense 20 € si on ne loue qu'un film (18 € d'abonnement + 2 € pour le film).

On dépense 22 € si on loue deux films (18 € d'abonnement + 20 € pour les deux films).

En examinant seulement les deux premières colonnes de nombres du tableau, on voit que ce n'est pas un tableau de proportionnalité. En effet : 20 = 1 × 20 et 22   2 × 20.

On en conclut que la dépense annuelle n'est pas proportionnelle au nombre de films loués.