Reconnaître des figures symétriques par rapport à un point

On sait qu'une figure est symétrique par rapport à une droite si, quand on la plie suivant cette droite, les deux parties de la figure se superposent.

Mais comment reconnaît-on une figure symétrique par rapport à un point ?

1. Définition

Soit F une figure et O un point. Dire que F est symétrique par rapport à O signifie que la figure symétrique de F par rapport à O est F elle-même. On dit alors que O est un centre de symétrie de F.

2. Exemples de figures symétriques par rapport à un point

2.1. Le segment

Le centre de symétrie d'un segment est le milieu de ce segment.

2.2. La droite

Tout point d'une droite est centre de symétrie de cette droite.

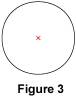
2.3. Le cercle

Le centre de symétrie d'un cercle est le centre de ce cercle.

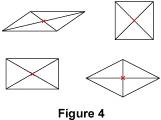
2.4. Le parallélogramme

Le centre de symétrie d'un parallélogramme, en particulier d'un carré, d'un rectangle ou d'un losange, est le point d'intersection de ses diagonales.

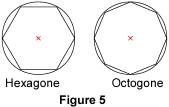
2.5. Les polygones réguliers

Le centre de symétrie d'un polygone régulier ayant un nombre pair de côtés est le centre du cercle circonscrit à ce polygone.

2.6. Autre cas

Considérons la figure F, comprenant deux segments [AB] et [DC] de même milieu O, et deux demi-cercles de diamètres respectifs [AO] et [OB].

On voit que le symétrique par rapport à O :

du demi-cercle de diamètre [AO] est le demi-cercle de diamètre [OB] ;

du demi-cercle de diamètre [OB] est le demi-cercle de diamètre [AO] ;

du segment [AB] est lui-même ;

du segment [CD] est lui-même.

Ainsi, le symétrique de la figure F par rapport à O est elle-même ; elle est donc symétrique par rapport à O.