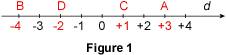
Ranger des nombres relatifs dans l'ordre croissant ou décroissant

Sur une carte météo, on peut lire les températures suivantes : -4 °C ; 0 °C ; +7 °C ; -12 °C ; +3 °C ; -9 °C ; +8 °C ; etc.

Quelle est la température la plus basse ? Quelle est la plus haute ?

Comment ranger ces températures de la plus basse à la plus haute ?

1. Comparer des nombres relatifs

1.1. En utilisant une droite graduée

La droite d représentée sur la figure ci-dessous est graduée ; on dit que c'est un axe.

Les nombres relatifs écrits sous cet axe sont les abscisses des points marqués sur la droite.

Par exemple, le point B a pour abscisse -4 ; le nombre +3 est l'abscisse du point A.

Sur cet axe, on considère qu'il y a un sens de parcours : de la gauche vers la droite ; ce sens est symbolisé par la flèche. Grâce à ce sens de parcours, on peut dire par exemple que B est avant le point A, ce que l'on traduit par -4 est inférieur à +3 et que l'on note : -4 < +3.

De même, B est avant D, et donc : -4 < -2.

Définition : soit A et B deux points d'un axe, d'abscisses respectives a et b. Dire que a est inférieur à b signifie que A est avant B. On note : a < b.

1.2. En appliquant des règles

Soit a et b deux nombres différents de 0. Si a est négatif et si b est positif, alors a < b.

Exemples : -25 < +34 ; -0,02 < +3,8.

Soit a et b deux nombres. Si a < b, alors -b < -a.

Exemples : 12 < 28, c'est-à-dire +12 < +28, donc : -28 < -12 ;

0,18 < 0,2 donc : -0,2 < -0,18.

2. Ranger des nombres relatifs

2.1. Dans l'ordre croissant

Dans l'ordre croissant signifie du plus petit au plus grand.

Considérons les nombres : -4 ; 0 ; +7 ; -12 ; +3 ; -9 ; +8 (voir les températures données dans l'exemple de l'introduction). On veut ranger ces nombres dans l'ordre croissant.

On cherche le plus petit nombre. C'est -12 car : -12 < -4 et -12 < 0 et -12 < +7, etc.

On barre -12 de la liste : -4 ; 0 ; +7 ; -12 ; +3 ; -9 ; +8.

On cherche le plus petit nombre parmi ceux qui restent. C'est -9.

On barre -9 de la liste : -4 ; 0 ; +7 ; -12 ; +3 ; -9 ; +8.

Et ainsi de suite.

On obtient successivement : -12 ; -9 ; -4 ; 0 ; +3 ; +7 ; +8.

Ainsi écrits, ces nombres sont rangés dans l'ordre croissant.

On peut aussi écrire : -12 < -9 < -4 < 0 < +3 < +7 < +8.

Remarque : on peut aussi commencer par séparer les nombres à ranger en deux groupes : les nombres strictement négatifs : -4, -12, -9, et les nombres positifs : 0, +7, +3, +8 ; on ordonne d'abord les nombres négatifs : -12 < -9 < -4, puis les positifs : 0 < +3 < +7 < +8.

On en déduit que : -12 < -9 < -4 < 0 < +3 < +7 < +8.

2.2. Dans l'ordre décroissant

Dans l'ordre décroissant signifie du plus grand au plus petit.

Reprenons l'exemple précédent. On veut ranger ces nombres dans l'ordre décroissant.

Si l'on connaît la liste des nombres dans l'ordre croissant, il suffit d'écrire cette liste à l'envers, ce qui donne : +8 ; +7 ; +3 ; 0 ; -4 ; -9 ; -12 ; ou encore : +8 > +7 > +3 > 0 > -4 > -9 > -12.

Si l'on ne connaît pas la liste des nombres dans l'ordre croissant, on procède comme dans le paragraphe précédent : on commence par chercher le plus grand nombre (+8) ; on le barre de la liste ; on cherche le plus grand nombre parmi ceux qui restent (+7) ; etc.